A statisztikus termodinamikai alapok

Tekintsünk egy V térfogatú, T hőmérsékletű, N részecskéből álló fluidumot. A rendszer egyensúlyi állapotban van, azaz a termodinamikai mennyiségek időben állandó egyensúlyi értékük körül fluktuálnak. A dinamikai mennyiségek mérhető értékei időátlagok, melyeket az ergodikus hipotézisnek megfelelően sokaság szerinti átlagolással helyettesíthetünk. A következő feltevésekkel élünk:

(1) Az i-edik kvantumállapot betöltési valószínűsége a rendszer energiájától függ a következő valószínűség-eloszlási törvény szerint:

ahol

a kanonikus állapotösszeg. Az összegzés az összes kvantumállapotra történik. Amennyiben a rendszert klasszikus mechanikai eszközökkel irjuk le, a Hamilton-operátor sajátértékei helyett a rendszer Hamilton-függvényét kell ismernünk a fázistér felett. A fázistér NF dimenziós, ahol F egy részecske külső (transzlációs és rotációs) szabadsági fokainak a száma. (Ez 3 gömbszimmetrikus, 5 lineáris, 6 nemlineáris molekulák esetében.) Az állapotösszeg helyébe ekkor a következő integrál lép:

Az integrálás a teljes fázistérre történik. Ez az ún. Boltzmann-statisztika, ami a Bose-Einstein statisztika magas hőmérsékletű határesete, és kb. 20 K fölött nyújtja pontos leírását az anyagi rendszereknek.

(2) Feltesszük, hogy a belső, intramolekuláris (rezgés, belső forgás) és a külső, tömegközépponti (transzláció, külső forgás, intermolekuláris kölcsönhatások) mozgásformák függetlenek egymástól. Ekkor a Hamilton-operátor két, egymástól független részre osztható: . Ennek megfelelően az állapotösszeg is szeparálható: . Feltesszük, hogy független a rendszer sűrűségétől, azaz ideális gázban ugyanakkora, mint folyadékban. Nagy sűrűségeknél, többatomos molekulák esetében ez a feltétel hibákat okozhat.

(3) A következő lépésben feltételezzük, hogy a külső mozgásformák is faktorizálhatók, azaz felírható a transzlációs, rotációs és a molekulák közötti kölcsönhatásból származó járulékok összegeként. Ekkor a tömegközépponti állapotösszegre kapjuk, hogy , ahol a transzlációs, a rotációs és a konfigurációs állapotösszeg.

(4) Nem túl alacsony hőmérsékleten ezek a mozgásformák klasszikusan kezelhetők. (A belső mozgásformákat általában kvantummechanikai eszközökkel írják le.) A molekulák közötti kölcsönhatásból származó, konfigurációs mennyiségek meghatározására szorítkozunk. A konfigurációs állapotösszeg:

ahol a teljes térszög (lineáris molekulákra , nemlineárisakra ), a konfigurációs integrál és a potenciális (konfigurációs) energia. A termodinamikai mennyiségek az állapotösszegekből a szokásos módon származtathatók. A konfigurációs mennyiségek például a konfigurációs integrálból a következőképpen:

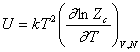
(5) Feltesszük, hogy a potenciális energia páronként additív, azaz a teljes energia a különálló párok kölcsönhatási energiáinak összege:

Ez nagyobb sűrűségeknél hibákhoz vezethet.

A konfigurációs állapotösszeg nehezen kezelhető mennyiség. A páronkénti additivitás feltételezésével azonban egy olyan függvény származtatható, amely segítségével a termodinamikai jellemzők szintén számolhatók és az elméleti módszerekben nagy jelentősége van. A szögfüggő párkorrelációs függvény definíció szerint

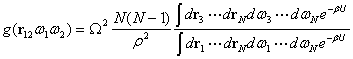
amit szög szerint átlagolva a radiális eloszlásfüggvényhez jutunk. (Gyakran csak ezt nevezik párkorrelációs függvénynek; a továbbiakban, ha nem jelezzük külön, ezt fogjuk érteni párkorrelációs függvény alatt.) arányos annak valószínűségével hogy valamely központi részecskétől r távolságban az gömbhéjban részecskét találunk. A párkorrelációs függvény a következő kapcsolatban van a lokális részecskeszám-sűrűséggel: . Folyadékokban és gázokban röntgen- vagy neutrondiffrakciós kísérletekkel meghatározható.

Amikor egy rendszert vizsgálunk, rögzíteni kell annak termodinamikai határfeltételeit, azaz hogy a rendszert milyen tulajdonságú falak határolják. Eszerint különféle sokaságokat lehet definiálni. Ebben a dolgozatban háromféle sokaság fordul elő, röviden vázoljuk ezek tulajdonságait, megadjuk a kváziklasszikus konfigurációs állapotösszegeket és a sokaságátlagokat.

(1) A fenti meggondolásokat a kanonikus (NVT) sokaságra vezettük végig. Itt a diaterm, merev és impermeábilis fallal határolt rendszer T hőmérsékletű hőtartállyal érintkezik. A konfigurációs kanonikus állapotösszeg, melyet a továbbiakban -vel jelölünk, a (2.1.4) egyenlettel adott. Legyen valamely, csak a konfigurációs koordinátáktól függő dinamikai mennyiség. Ennek NVT-sokaságon vett átlaga:

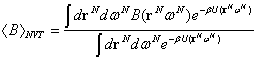
(2) Amennyiben a rendszer nyomását tartjuk állandó értéken a térfogata helyett, azaz a fal elmozdítható, akkor az izoterm-izobár (NpT) sokasághoz jutunk. NpT-sokaságon a konfigurációs állapotösszeg

a B konfigurációs fizikai mennyiség átlaga pedig

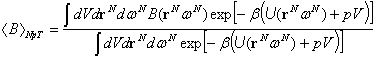
(3) A nagykanonikus (GC) sokaság nyitott, a fal diaterm, merev és permeábilis, az állandó értéken tartott termodinamikai paraméterek a hőmérséklet, a térfogat és a kémiai potenciál (). A konfigurációs nagykanonikus állapotösszeg

az átlagképzés GC-sokaságon

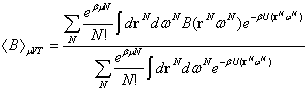
Megkülönböztetünk konfigurációs, teljes, ideális és reziduális mennyiségeket. A konfigurációs mennyiségek a konfigurációs integrálból származnak a (2.1.5) egyenletek szerint, míg a rezudális mennyiségek a teljes és az ideális mennyiségek különbségeként állnak elő. Mivel a disszertációban konfigurációs mennyiségekkel foglalkozunk, ezeket nem indexeljük , míg a másik hármat a t, id és r felső indexekkel jelöljük. Az energia, az entalpia és a kémiai potenciál esetében ezek között a következő összefüggések állnak fenn:

A dinamikai nyomás

ahol W az ún. viriálösszeg, amely az energia V szerinti deriváltjával van összefüggésben a következő módon:

ahol felhasználtuk, hogy . A nyomás V szerinti deriváltjának számolásánál (NVT+TP és GC módszerek) jelentősége lesz az X hiperviriálnak és az Y második hiperviriálnak (ez utóbbira az irodalomban nem találtunk elnevezést). Ezek a viriál első és második deriváltjaival arányosak és a definíciójuk: