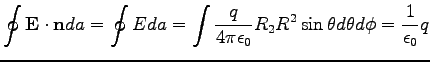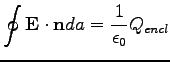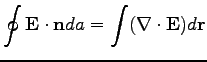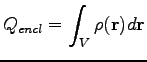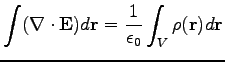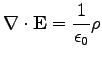

Next: Elektrosztatika anyagban
Up: Elektrosztatika vákuumban
Previous: Folytonos töltéseloszlások
Könnyebb lesz eljutni a célunkhoz, ha definiálunk néhány hasznos fogalmat.
Először is néhány szó az erővonalakról.
Ezek főleg vizuális emberek számára jelentenek könnyebbséget a dolgok megértéséhez.
Ezek az erővonalak mindig a térerősségek mentén futnak.
Egy ponttöltésből pl. sugárirányban kifelé.
Ez példa mutatja, hogy a erővonalak iránya a térerősség irányát definiálja, míg az erővonalak sűrűsége a térerősség nagyságát.
A ponttöltéstől  távolságban ugyanis az erővonalak sűrűsége
távolságban ugyanis az erővonalak sűrűsége 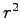 -tel fordított arányban csökken, mivel a felület
-tel fordított arányban csökken, mivel a felület 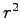 -tel arányosan nő.
De a térerősség is
-tel arányosan nő.
De a térerősség is 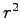 -tel fordított arányban csökken.
-tel fordított arányban csökken.
Az előadáson több példát felrajzolok majd, itt most inkább rátérek egy másik segédfogalom definiálására.
A fluxus egy 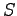 felületen keresztül nem más, mint a térerősség normálisának integrálja a felületen:
felületen keresztül nem más, mint a térerősség normálisának integrálja a felületen:
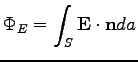 |
(40) |
ahol
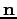 a felület normálvektora, azaz a felületre merőleges egységvektor.
Látható, hogy a fluxus a felületen áthaladó erővonalak számával arányos.
a felület normálvektora, azaz a felületre merőleges egységvektor.
Látható, hogy a fluxus a felületen áthaladó erővonalak számával arányos.
Számítsuk ki egy 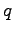 ponttöltés terének fluxusát egy
ponttöltés terének fluxusát egy 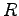 sugarú gömbön, aminek a középpontjában a töltés helyezkedik el.
sugarú gömbön, aminek a középpontjában a töltés helyezkedik el.
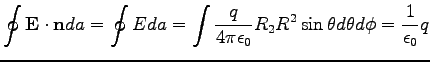 |
(41) |
Az első lépésben vektorok helyébe skalárt írtunk, mivel a gömb felületén a tér mindig a felületre merőleges.
Rendkívül fontos, hogy 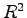 kiesik, ami azt eredményezi, hogy az eredmény nem függ a gömb sugarától.
Megmutatható, hogy bármilyen, a
kiesik, ami azt eredményezi, hogy az eredmény nem függ a gömb sugarától.
Megmutatható, hogy bármilyen, a 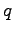 töltés körüli zárt felületre integrálhatunk, az eredmény ugyanaz.
Sőt, a szuperpozíció elvét felhasználva, az is következik, hogy a zárt felületen belül akármennyi töltés lehet, a eredmény megint csak ugyanaz.
Ez Gauss törvénye: bármely zárt felületen számított fluxus arányos a felület által bezárt töltéssel:
töltés körüli zárt felületre integrálhatunk, az eredmény ugyanaz.
Sőt, a szuperpozíció elvét felhasználva, az is következik, hogy a zárt felületen belül akármennyi töltés lehet, a eredmény megint csak ugyanaz.
Ez Gauss törvénye: bármely zárt felületen számított fluxus arányos a felület által bezárt töltéssel:
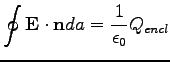 |
(42) |
Fontos hangsúlyozni, hogy a törvény levezetéséhez továbbra is csak a Coulomb-törvény és a szuperpozíciüó elve szükséges.
A divergenciatétel (amit neveznek Gauss-tételnek is) használatával ez az integrális forma differenciális egyenletté alakítható.
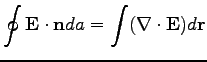 |
(43) |
ahol a 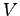 térfogat az
térfogat az 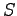 felület határolt tér.
A töltést megkaphatjuk a töltéssűrűség integráljaként:
felület határolt tér.
A töltést megkaphatjuk a töltéssűrűség integráljaként:
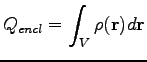 |
(44) |
Ebből
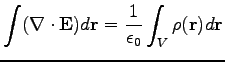 |
(45) |
Mivel a 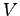 térfogat tetszőleges, a két integrál egyenlő, ha az integraduszok egyenlők:
térfogat tetszőleges, a két integrál egyenlő, ha az integraduszok egyenlők:
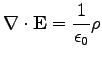 |
(46) |
Ez Gauss törvényének differenciális alakja és mellesleg a első Maxwell-egyenlet.
Előnye, hogy lokális, nem függ a felület definíciójától.
Gyakorlati alkalmazásokban az integrális alakot használjuk.


Next: Elektrosztatika anyagban
Up: Elektrosztatika vákuumban
Previous: Folytonos töltéseloszlások
Dezso Boda
2006-08-30
![]() távolságban ugyanis az erővonalak sűrűsége
távolságban ugyanis az erővonalak sűrűsége ![]() -tel fordított arányban csökken, mivel a felület
-tel fordított arányban csökken, mivel a felület ![]() -tel arányosan nő.
De a térerősség is
-tel arányosan nő.
De a térerősség is ![]() -tel fordított arányban csökken.
-tel fordított arányban csökken.
![]() felületen keresztül nem más, mint a térerősség normálisának integrálja a felületen:
felületen keresztül nem más, mint a térerősség normálisának integrálja a felületen:
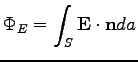
![]() ponttöltés terének fluxusát egy
ponttöltés terének fluxusát egy ![]() sugarú gömbön, aminek a középpontjában a töltés helyezkedik el.
sugarú gömbön, aminek a középpontjában a töltés helyezkedik el.