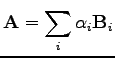

Next: Koordinátarendszerek
Up: Vektorkalkulus
Previous: Vektorkalkulus
Négyféle vektorműveletet definiálunk, az összeadást és háromféle szorzást:
- Összeadás: paralelogramma szabály. Kommutatív:
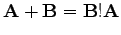 |
(1) |
és asszociatív:
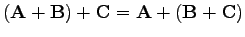 |
(2) |
- Skalárral való szorzás: a vektor hosszát változtatja, irányát nem (illetve negatív skalárral való szorzás a vektor irányát az ellenkező irányba változtatja). Disztributív:
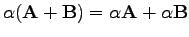 |
(3) |
A fenti kettőből adódik, hogy vektort úgy vonunk ki egy másikból, hogy hozzáadjuk az ellentettjét (-1-szeresét):
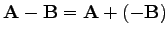 |
(4) |
A fenti két műveletet akárhányszor alkalmazhatjuk:
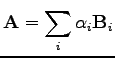 |
(5) |
ekkor azt mondjuk, hogy az
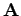 vektor az
vektor az
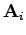 vektorok lineáris kombinációja.
vektorok lineáris kombinációja.
- Skalárszorzat: két vektor skalárszorzata a vektorok hosszának szorzata, szorozva az általuk bezárt szög koszinuszával
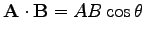 |
(6) |
A skalárszorzat kommutatív:
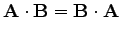 |
(7) |
és disztributív
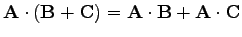 |
(8) |
Geometriai interpretáció:
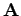 hossza szorova a
hossza szorova a
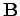 vektor
vektor
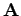 -ra eső vetületével.
Ha két vektor párhuzamos, akkor egyszerűen
-ra eső vetületével.
Ha két vektor párhuzamos, akkor egyszerűen
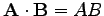 .
Egymásra merőleges vektorok skalárszorzata zérus.
Egy vektor önmagával vett skalárszorzata
.
Egymásra merőleges vektorok skalárszorzata zérus.
Egy vektor önmagával vett skalárszorzata
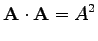 |
(9) |
ahonnan a vektor hossza
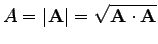 .
A vektorterek általános elméletében először definiálják a skalárszorzatot, majd annak segítségével definiálják a vektor hosszát.
Egységvektorról beszélünk, ha
.
A vektorterek általános elméletében először definiálják a skalárszorzatot, majd annak segítségével definiálják a vektor hosszát.
Egységvektorról beszélünk, ha
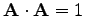
- Vektorszorzat: két vektor vektoriális szorzata
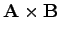 szintén egy vektor, melynek iránya az
szintén egy vektor, melynek iránya az
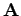 és
és
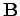 vektorok által kifeszített síkra merőleges mégpedig úgy, hogy
vektorok által kifeszített síkra merőleges mégpedig úgy, hogy
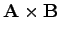 irányából nézve
irányából nézve
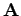 -t pozitív irányú (az óramutató járásával ellentétes) forgatással lehet
-t pozitív irányú (az óramutató járásával ellentétes) forgatással lehet
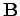 irányába forgatni (jobbkézszabály).
A vektoriális szorzat hossza
irányába forgatni (jobbkézszabály).
A vektoriális szorzat hossza
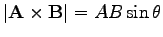 |
(10) |
A vektrorszorzás disztributív
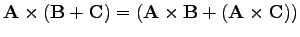 |
(11) |
de nem kommutatív
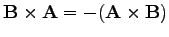 |
(12) |
Bármely vektor önmagával alkotott vektorszorzata nulla
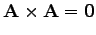 |
(13) |


Next: Koordinátarendszerek
Up: Vektorkalkulus
Previous: Vektorkalkulus
Dezso Boda
2006-08-30