Few theories have enjoyed the longevity
of the Poisson-Boltzmann (PB) theory that is now approaching its
centennial. However, its popularity may be due as much to
the ingenuity of its users in fitting parameters as to its
accuracy. This theory is based on the assumption that the
solvent in an electrolyte may be replaced by a dielectric
continuum whose dielectric constant,  , is equal to that
of the solvent, together with the combination of Poisson's equation,
, is equal to that
of the solvent, together with the combination of Poisson's equation,
![[del]<sup>2</sup><i>phi</i>(<i>r</i>) = -((4 <i>pi</i> <i>e</i>)/(<i>epsilon</i>)) [summation]<sub><i>i</i> = 1</sub><sup><i>m</i></sup><i>z</i><sub><i>i</i></sub><i>rho</i><sub><i>i</i></sub><i>g</i><sub><i>i</i></sub>(<i>r</i>),](7170_1m0.gif)
and the Boltzmann relation,
![<i>g</i><sub><i>i</i></sub>(<i>r</i>) = exp[-<i>beta</i> <i>z</i><sub><i>i</i></sub><i>e</i> <i>phi</i>(<i>r</i>)].](7170_1m1.gif)
The PB theory is employed in electrochemistry, where it
is known as the Gouy-Chapman (GC) theory,1,2
in solution chemistry, where it is known as the Debye-Hückel
(DH) theory,3 in colloidal chemistry, where it is known as
the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory,4,5
and in biophysics,6,7 where it is known
simply as the PB theory. The emphasis here is on the
electrochemical application. However, we expect that our conclusions
will have broader implications.
In Eqs. (1)
and (2), m is the number of species
of ions in the electrolyte, 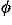 (r) is the electrostatic potential
at a distance r from a central ion, e is the
magnitude of the electronic charge, zi
and
(r) is the electrostatic potential
at a distance r from a central ion, e is the
magnitude of the electronic charge, zi
and 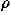 i
= Ni/V are the valence, including sign, and
number density of an ion of species i, and
i
= Ni/V are the valence, including sign, and
number density of an ion of species i, and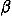 = 1/kT, k,
being the Boltzmann constant. The function gi(r)
is the normalized local density of an ion of species i at
a distance r from a central ion. The quantities, V,T,
and Ni are the volume, temperature, and number of
ions of species i, respectively. Gaussian (cgs) units are employed.
The difference in the formulas if rationalized MKS units are
used is slight.
= 1/kT, k,
being the Boltzmann constant. The function gi(r)
is the normalized local density of an ion of species i at
a distance r from a central ion. The quantities, V,T,
and Ni are the volume, temperature, and number of
ions of species i, respectively. Gaussian (cgs) units are employed.
The difference in the formulas if rationalized MKS units are
used is slight.
This study is devoted to the study
of the accuracy of the PB theory for a system of ions in a
model dielectric continuum. This model is called the
primitive model (PM), a name that is well chosen. The
question of whether it is reasonable to consider a solvent
as a dielectric continuum is considered briefly at the end
of this article.
One can hardly question Eq.
(1), as it is equivalent to Coulomb's law. However, as
is seen from the arguments of Henderson and Blum,8,9 Eq.
(2) makes sense only for point ions. In reality, ions
have a nonzero size. In this work, we assume that all the
ions have the same diameter, d. This simplified PM
with ions of equal size is called the restricted primitive
model (RPM). Point ions are not just a simplification; they
are a potential disaster because the Coulomb interaction will
diverge at r = 0. This disaster is averted in part by
giving the central ion (the electrode in electrochemistry) a finite
size. However, it is at best illogical to give a size to one
ion and ignore the size of all other ions; at worst, quite
incorrect results might be obtained. Clearly, a
self-consistent theory is preferable.
The PB/GC theory predicts
a layer of counterions near the electrode. This layer and
the layer of charge in the electrode form what is called a
double layer. By itself, the PB/GC theory gives poor
results. The PB/GC theory is made useful by postulating what
is variously called a Stern layer, or Helmholtz layer, or
compact layer, or inner layer. The idea is that the center
of charge of the ions cannot come right to the electrode but
are prevented from doing so not only by their own radius, d/2,
but also by a solvation layer of solvent, usually water,
molecules. In electrochemical applications, the properties
of this layer are expressed in terms of parameters, some of
dubious physical significance, whose values are adjusted to
fit the experiment. The idea is that the PB/GC theory is
accurate for the region beyond the Stern layer, that is
called the diffuse layer.
This means that, because
of the use of adjustable parameters, the accuracy of the
PB/GC theory cannot be determined by comparison with experiment. The
first unambiguous test of the PB/GC theory was made by
Torrie and Valleau (TV)10,11 almost 20 years ago in an
important series of Monte Carlo (MC) simulations, that apart from
statistical uncertainties are exact, for monovalent and divalent ions of
diameter d = 4.25 Å. Even with this rather large diameter,
their results showed more disagreement with the PB/GC theory
than they commented upon. Following their work, studies (at
least simulation studies) were discontinued for a rather
lengthy period. Recently, we have returned to such
simulation studies. We have considered solvent effects,12 molten salt double layers,13 and double layers at low (effective or
dimensionless) temperatures14 and have found that the
PB/GC theory has problems in describing the behavior of
these systems. Also, we have applied density functional
theory (DFT) to the PM double layer in molten salts and
aqueous electrolytes at low effective temperatures15 and to a related membrane problem.16,17
Density functional theory
is a type of integral equation theory for an inhomogeneous
fluid, based on a second-order density functional expansion in the
difference, 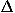
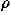 i(r)
=
i(r)
= 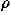 i(r)-
i(r)-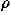 i,
of the inhomogeneous density from the uniform reference
density, yielding, after minimization of the free energy, an integral
equation that is somewhat similar in form to less successful
integral equations, such as the hypernetted chain (HNC) approximation equation.
As is common with integral equations for inhomogeneous fluids, the
DFT equation requires as input the direct correlation function (dcf)
of the uniform fluid. Because DFT is quite standard, we
refer to the paper of Rosenfeld18 for details. Why DFT
should be more accurate than say the HNC theory even when
the density inhomogeneities are very large as is the case
here, is far from clear. Certainly, the use of a nonlocal
density is crucial. Anyway, one cannot argue with success.
i,
of the inhomogeneous density from the uniform reference
density, yielding, after minimization of the free energy, an integral
equation that is somewhat similar in form to less successful
integral equations, such as the hypernetted chain (HNC) approximation equation.
As is common with integral equations for inhomogeneous fluids, the
DFT equation requires as input the direct correlation function (dcf)
of the uniform fluid. Because DFT is quite standard, we
refer to the paper of Rosenfeld18 for details. Why DFT
should be more accurate than say the HNC theory even when
the density inhomogeneities are very large as is the case
here, is far from clear. Certainly, the use of a nonlocal
density is crucial. Anyway, one cannot argue with success.
The value d = 4.25
Å that was used by TV is somewhat large. Presumably,
this value was chosen to be representative of a solvated
ion. Here, we examine the GC theory for d = 3
Å. In addition, we consider DFT for ions with this
smaller diameter. We do not use a compact layer with
adjustable parameters. The ions, including those treated by the
PB/GC theory, can approach to a distance d/2 from the
electrode. The dielectric constant within this inner layer is equal
to that in the diffuse layer.
THEORETICAL CONSIDERATIONS
The electrochemical interface
is examined at room temperature with the dielectric constant of
water, and d = 3 Å. Specifically, for an i,j
pair, we use the dimensionless or reduced coupling
constant, 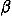 zizje2/
zizje2/ d =
2.3811zizj, or, equivalently, the
dimensionless temperature, T* =
d =
2.3811zizj, or, equivalently, the
dimensionless temperature, T* =  dkT/e2
= 0.419 95. Our earlier studies have shown that the smaller
the value of T*, or the larger the value
of the coupling constant, the greater the errors in the
PB/GC theory. Since a large coupling constant can be achieved
by reducing the temperature, the dielectric constant, or value ofd,
the value that is used here for d is likely to yield
more interesting results than that used by TV. If the reader
prefers rationalized MKS units, the definition of the
dimensionless coupling constant is
dkT/e2
= 0.419 95. Our earlier studies have shown that the smaller
the value of T*, or the larger the value
of the coupling constant, the greater the errors in the
PB/GC theory. Since a large coupling constant can be achieved
by reducing the temperature, the dielectric constant, or value ofd,
the value that is used here for d is likely to yield
more interesting results than that used by TV. If the reader
prefers rationalized MKS units, the definition of the
dimensionless coupling constant is 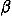 zizje2/4
zizje2/4
 0
0 d and the dimensionless
temperature is T* = 4
d and the dimensionless
temperature is T* = 4
 0
0 dkT/e2.
The numerical values of these dimensionless quantities is the
same in both systems of units.
dkT/e2.
The numerical values of these dimensionless quantities is the
same in both systems of units.
There are three exact
results that can be used to assess a theory. The first is
electroneutrality,
![<i>e</i>[summation]<sub><i>i</i> = 1</sub><sup><i>m</i></sup><i>z</i><sub><i>i</i></sub><i>z</i><sub><i>j</i></sub>[integral]<sub>0</sub><sup>[infinity]</sup><i>g</i><sub><i>i</i></sub>(<i>t</i>)<i>d</i><i>t</i> = -<i>sigma</i>,](7170_1m2.gif)
where  is the charge per unit area on the electrode
surface. That is, the charge in the double layer must be the
negative of that of the electrode. All acceptable theories,
including PB/GC, satisfy this condition. As a result, we
will not emphasize this test. The second is the contact
value condition of Henderson et al.,19
is the charge per unit area on the electrode
surface. That is, the charge in the double layer must be the
negative of that of the electrode. All acceptable theories,
including PB/GC, satisfy this condition. As a result, we
will not emphasize this test. The second is the contact
value condition of Henderson et al.,19
![<i>k</i><i>T</i>[summation]<sub><i>i</i> = 1</sub><sup><i>m</i></sup> <i>rho</i><sub><i>i</i></sub>(<i>d</i>/2) = <i>p</i>+((2 <i>pi</i> <i>sigma</i><sup>2</sup>)/(<i>epsilon</i>)),](7170_1m3.gif)
where 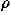 i(t)
=
i(t)
= 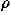 igi(t)
and p is the pressure of the bulk electrolyte. This
contact value condition is a force balance condition. The
momentum transfer at the electrode must equal p plus
the Maxwell stress. The corresponding PB/GC result is
igi(t)
and p is the pressure of the bulk electrolyte. This
contact value condition is a force balance condition. The
momentum transfer at the electrode must equal p plus
the Maxwell stress. The corresponding PB/GC result is
![<i>k</i><i>T</i>[summation]<sub><i>i</i> = 1</sub><sup><i>m</i></sup> <i>rho</i><sub><i>i</i></sub>(<i>d</i>/2) = <i>k</i><i>T</i>[summation]<sub><i>i</i> = 1</sub><sup>[infinity]</sup> <i>rho</i><sub><i>i</i></sub>+((2 <i>pi</i> <i>sigma</i><sup>2</sup>)/(<i>epsilon</i>)).](7170_1m4.gif)
Because of the absence of an explicit solvent, the PM electrolyte
is normally at a low-density system. Thus, at room temperatures
and electrolyte concentrations, the pressure is close to that of
an ideal gas and the PB/GC result for the charge profile at
contact is nearly correct and becomes increasing accurate as
the charge of the electrode is increased and the second term
on the right-hand side of Eqs. (4) and (5) becomes dominant. The third is the set of MC
results. As we have commented, apart from statistical uncertainties, these
results are exact.
If the MSA bulk electrolyte dcf is
used as input, is the corresponding DFT contact value condition
is
![<i>k</i><i>T</i>[summation]<sub><i>i</i> = 1</sub><sup><i>m</i></sup> <i>rho</i><sub><i>i</i></sub>(<i>d</i>/2) = <i>a</i>+((2 <i>pi</i> <i>sigma</i><sup>2</sup>)/(<i>epsilon</i>)).](7170_1m5.gif)
The exact expression for a has not been determined
but, numerically, it appears to be some function of the MSA
compressibility. If an exact bulk electrolyte dcf is used as
input, a = p should follow and the DFT contact value
should be exact. We have verified numerically that, if the
generalized MSA (GMSA) dcf, which is not exact, is used, Eq.
(6) is satisfied with a being some function ofp,
where p is the MSA pressure. In summary, the DFT
satisfies the contact value condition in a manner that is
related to the level of accuracy of the input MSA. The GMSA
improvement will be discussed elsewhere; it is not an
important issue for the system considered here since p, 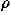 kT, and the
inverse compressibility are nearly equal in the PM for the
conditions considered here. Differences would be apparent
when a molecular solvent is considered, at molten salt
densities, or at low effective temperatures (or, equivalently, high coupling
constants).
kT, and the
inverse compressibility are nearly equal in the PM for the
conditions considered here. Differences would be apparent
when a molecular solvent is considered, at molten salt
densities, or at low effective temperatures (or, equivalently, high coupling
constants).
At this point, a few comments
about the first two conditions are in order. Henderson has
commented at the Southampton (1984) and Berlin (1986)
electrochemistry meetings that since the PB/GC satisfies the
first condition and nearly satisfies the second condition
(in the PM at small coupling constants), the PB/GC charge
profile starts with nearly the correct contact value and has
the correct area (electroneutrality) and, therefore, cannot give terrible
results for the profiles and potential. Stated this way, the
observation is correct. However, this argument has been repeated frequently
by others as an argument supporting the idea that the PB/GC
is reliable, a conclusion that was never intended when the
argument was stated and is frequently unjustified. Since we
are on this subject, it is to be noted that whatever the
merits of this observation, it is applicable only for the PM
and has uncertain merit for real systems with a solvent.
We note that the choice of the
variable that specifies the system is arbitrary. In simulations, it
is convenient to specify the charge on the electrode. However,
in many integral equation theories and in DFT calculations the
electric potential of the electrode is a more convenient variable.
Using the potential as the variable and assuming, for simplicity,
that m = 2 and the ions are monovalent, the PB/GC contact
value condition is
![<i>g</i><sub><i>i</i></sub>(<i>d</i>/2) = exp[-<i>beta</i> <i>e</i> <i>phi</i>(<i>d</i>/2)]](7170_1m6.gif)
or
![<i>k</i><i>T</i>[summation]<sub><i>i</i> = 1</sub><sup>2</sup> <i>rho</i><sub><i>i</i></sub><i>g</i><sub><i>i</i></sub>(<i>d</i>/2) = <i>rho</i> <i>k</i><i>T</i> cosh[<i>beta</i> <i>e</i> <i>phi</i>(<i>d</i>/2)],](7170_1m7.gif)
where 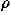 =
= ![[summation]](sum.gif)
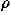 i.
Equation (8) is equivalent to Eq. (5) only if the relation between
i.
Equation (8) is equivalent to Eq. (5) only if the relation between  and
and 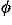 (d/2) that
is given by the PB/GC theory is accurate. If this relation
is not accurate, we know from the contact value theorem and
Eq. (5) that it is better to use charge
rather than potential as the variable. However, from the
point of view of logic there is no reason to make this
choice. In fact, within the PB/GC theory, the potential
seems more logical variable since it is the potential that
appears in the formulation of the PB/GC theory, Eq. (2), and many of the results of this theory,
especially for asymmetric electrolytes, are expressed more compactly if
the potential is used as the variable. In this paper, the
PB/GC theory and the DFT will be tested using both the
charge and potential as the variable that specifies the
system.
(d/2) that
is given by the PB/GC theory is accurate. If this relation
is not accurate, we know from the contact value theorem and
Eq. (5) that it is better to use charge
rather than potential as the variable. However, from the
point of view of logic there is no reason to make this
choice. In fact, within the PB/GC theory, the potential
seems more logical variable since it is the potential that
appears in the formulation of the PB/GC theory, Eq. (2), and many of the results of this theory,
especially for asymmetric electrolytes, are expressed more compactly if
the potential is used as the variable. In this paper, the
PB/GC theory and the DFT will be tested using both the
charge and potential as the variable that specifies the
system.
The MC simulations were
performed using the method that is discussed in detail in
our previous papers;12,13 this
discussion is not repeated here. The MC calculations were performed
on a SGI Power Challenge computer (R10000 chip).
The DFT calculations
were based on the method of Rosenfeld19
that is outlined in our membrane study,16,17 assuming that the two walls of that
study are far apart and the wall is so thick that the fluids
on either side of the wall are independent of each other. We
refer the reader to these two papers. The DFT calculations
were performed with a Pentium III laptop.
RESULTS
The MC values of the charge and potential
are listed in Tables I and II. An electrode surface
charge density of 0.1 Cl/m2 is equal to  *=0.0562. A
concentration of 1 M is equal to a dimensionless density
of
*=0.0562. A
concentration of 1 M is equal to a dimensionless density
of 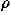 *=0.0162,
for the least abundant species. The PB/GC and DFT results
for these quantities for a 1:1 electrolyte are compared with
these MC results in Fig. 1 with parts (a) and (b)
giving the potential of the electrode,
*=0.0162,
for the least abundant species. The PB/GC and DFT results
for these quantities for a 1:1 electrolyte are compared with
these MC results in Fig. 1 with parts (a) and (b)
giving the potential of the electrode,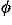 (0), and the diffuse layer potential,
(0), and the diffuse layer potential, 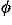 (d/2),
respectively, as functions of
(d/2),
respectively, as functions of  . The PB/GC potentials are
uniformly too large. On the other hand, the DFT results are
quite good. A comparison of the PB/GC and DFT profiles with
the MC results for a 1:1 electrolyte is given in Fig. 2, with
parts (a) and (b) making the comparison for the same
electrode charge and the same diffuse layer potential, respectively. The
PB/GC theory is somewhat better when the comparison is made
at the same electrode charge, but even then the PB/GC results
are still unsatisfactory. No matter what method is used for
the comparison, the DFT theory is in quite good agreement
with the MC results. These results are similar to those
reported for 1:1 electrolytes for d = 4.25 Å by TV, who
made comparisons of the profiles only for equal electrode charge.
In the TV simulations, the potential for a 1:1 electrolyte
rises strongly at (unphysically) large electrode charge densities and crosses
the PB/GC results, giving the illusion that the PB/GC theory
is not so bad. However, the MC counterion profile contains a
second layer.12 This is seen in DFT,19 but not in the PB/GC theory.
Presumably, a second layer would also be seen at large
charge densities with the MC and DFT techniques for the
system considered here. We do not pursue this question since
unphysically large charges and potentials are involved.
. The PB/GC potentials are
uniformly too large. On the other hand, the DFT results are
quite good. A comparison of the PB/GC and DFT profiles with
the MC results for a 1:1 electrolyte is given in Fig. 2, with
parts (a) and (b) making the comparison for the same
electrode charge and the same diffuse layer potential, respectively. The
PB/GC theory is somewhat better when the comparison is made
at the same electrode charge, but even then the PB/GC results
are still unsatisfactory. No matter what method is used for
the comparison, the DFT theory is in quite good agreement
with the MC results. These results are similar to those
reported for 1:1 electrolytes for d = 4.25 Å by TV, who
made comparisons of the profiles only for equal electrode charge.
In the TV simulations, the potential for a 1:1 electrolyte
rises strongly at (unphysically) large electrode charge densities and crosses
the PB/GC results, giving the illusion that the PB/GC theory
is not so bad. However, the MC counterion profile contains a
second layer.12 This is seen in DFT,19 but not in the PB/GC theory.
Presumably, a second layer would also be seen at large
charge densities with the MC and DFT techniques for the
system considered here. We do not pursue this question since
unphysically large charges and potentials are involved.
 Figure
1.
Figure
1.  Figure
2.
Figure
2.
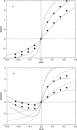
A similar comparison is made in
Figs. 3 and 4 for the 2:1
electrolyte. If the monovalent ions are the counterions, the
results are much like those of the 1:1 case. However, the
results for the case where the counterions are divalent is
more interesting. As a result, profiles for the 2:1
electrolyte case are shown only for the case of divalent
counterions. The PB/GC potentials lie above the MC results
but by a greater degree than for the monovalent case. The
DFT results are quite good. It is interesting to note that
the MC and DFT diffuse layer potentials pass through a
minimum and then increase, even to the extent that they
change sign. The MC and DFT profiles for the divalent
counterion case show charge inversion or charge
oscillations. Farther from the electrode, the coion profile exceeds
the counterion profile and the double layer has become a
triple layer. The PB/GC results for the profiles are poor.
They are particularly unsatisfactory if the comparison is made at
the same diffuse layer potential [Fig. 4(b)]. The DFT is
insensitive to this issue.
 Figure
3.
Figure
3.  Figure
4.
Figure
4.
These divalent counterion
results are similar to but more extreme than the results
reported by TV. In the TV study, the MC diffuse layer
potential for divalent counterions levels off. There is a
hint of a minimum and change of sign in the diffuse layer potential
in the TV MC results, but its possible existence is obscured
by statistical uncertainties.
DISCUSSION
Simulation results and the
results of PB/GC theory and DFT for charged hard sphere ions
in a dielectric medium (PM) are reported for spheres of
diameter 3 A. This was expected to be a more severe test
than the TV simulations that were performed for spheres of
diameter 4.25 A. Simulations results are a `gold standard'
against which theory may be tested without any uncertainty
regarding whether the PM is representative of experimental systems.
Density functional theory is
quite accurate. In contrast, the PB/GC theory is not very
successful. It consistently underestimates the magnitude of
the electrostatic potential for a given charge density on
the electrode. The errors in the PB/GC theory are even more
apparent when divalent ions are present. When the divalent
ions are the counterions, the MC and DFT diffuse layer
potentials pass through a minimum and then increase and can
even change sign. This means that the diffuse layer differential
capacitance is infinite and then changes sign and becomes negative.
Perhaps, the reader may be surprised by this result and may
feel that it is unphysical. However, there is no law of
nature that is violated. All that is assumed in the
simulations is Poisson's equation and the Gibbs' expression
for the probability distribution of a canonical ensemble. It is
interesting to note that a negative contribution to the capacitance
occurs in the study of the contribution of the metal
electrons to the capacitance;20 a reversal of the potential has
been seen in our previous work on membranes17
and in simulations of polyelectrolytes.21
A negative diffuse layer
differential capacitance means that the exotic mechanisms
that are invented22 to account for
decreases in the differential capacitance at higher potentials may be
unnecessary and may have the status of Ptolemy's epicycles. More
importantly, electrochemical reactions take place at or near the distance
of closest approach and requires an accurate result for the
potential for that point. This means that theories of electrochemical
reactions that employ the PB/GC theory are of uncertain accuracy.
This is especially true for reactions involving a multivalent ion
in a 1:1 electrolyte. For example, many experimental data involve
studies of the kinetics of transition metal 3+/2+ systems with
a 1:1 supporting electrolyte. In the past, the presence of
the foreign reactant in an otherwise simple 1:1 electrolyte has
been treated in an overly simplified way. A proper analysis
of such a system requires the application of more accurate
approximations to a MIXED electrolyte system. To the best of
our knowledge, this type of calculation has not been undertaken
yet.
The stronger the coupling or the
lower the effective (dimensionless or reduced) temperature,
the greater the errors in the PB/GC theory. It should be
noted that the differences seen here between simulations and
the PB/GC theory are but the beginnings of the large
differences we have seen at low effective temperatures,
where, among other things, the PB/GC theory predicts an
incorrect negative sign for the temperature derivative of the
capacitance.14 A positive temperature
derivative for the capacitance has been seen in the
experimental results of Hamelin et al.23
for frozen electrolytes. Also, unexpected results, possibly
due to large errors in the PB/GC theory, have been seen in
the experimental results for 3:1 electrolytes of Andreu and
Molero,24 who have studied the
differential capacity of dilute solutions of LaCl3 at far
negative electrode charge densities (<-20 µC/cm2).
However, the possibility that the double layer is not stable
when cations of large charge are forced into the double
layer cannot be discounted. In this connection, an extension
of our simulations and DFT calculations to 3:1 electrolytes,
where we expect even larger differences from the PB/GC
theory, than those seen here, may be of value.
The MC and DFT are both good approaches.
Regrettably, the PB/GC is unsatisfactory. The study here is based
on the use of the PM (or RPM). Real electrolytes are
dissolved in molecular solvents, not dielectric continua. Although under
some circumstances a dielectric constant may give a reasonable description
of the dielectric aspects of a solvent, the PM neglects the
fact that solvent molecules occupy space. This causes the
local density and potential profiles to oscillate with the result
that the local environment in an electrolyte modeled using a
reasonable model for the solvent is quite different from the
PM, even if the PM is treated accurately (see Figs. 4 and 5
of the review of Schmickler and Henderson.25 These effects are real and are seen in
experiment.26,27 It is time to use a
molecular solvent in electrochemical theory. To do this with
a highly accurate model for (say) water would be difficult.
However, the use of a hard sphere solvent with a dielectric
background, the solvent primitive model, is no more
difficult than the primitive model with a nonzero ionic
diameter and captures much of this behavior.12,28,29,30,31 Electrochemists
should adopt these concepts.
ACKNOWLEDGMENTS
This work was supported
in part by the National Science Foundation (Grant No.
CHE98-13729) and NATO (Grant No. HTECH CRG972915).
REFERENCES
- G. Gouy, J. Phys. (France) 9, 457
(1910). first citation in article
- D. L. Chapman, Philos. Mag. 25, 475
(1913). first citation in article
- P. Debye and E. Hückel, Physik 24,
185 (1923). first citation in article
- B. V. Derjaguin and L. Landau, Acta
Physicochim. USSR 14, 633 (1941). first
citation in article
- E. J. W. Verwey and J. Th. G. Overbeek, Theory
of the Stability of Lyophobic Colloids (Elsevier, Amsterdam, 1948). first citation in article
- M. E. Davis and J. A. McCammon, Chem. Rev. 90,
509 (1990). first citation in article
- B. Honig and A. Nichols, Science 268,
1144 (1995).first citation in article
- D. Henderson and L. Blum, J. Electroanal. Chem. 93,
151 (1978). first citation in article
- D. Henderson and L. Blum, J. Chem. Phys. 70,
3149 (1979). first citation in article
- G. M. Torrie and J. P. Valleau, J. Chem. Phys. 73,
5807 (1980). first citation in article
- G. M. Torrie and J. P. Valleau, J. Phys. Chem. 86,
3251 (1982). first citation in article
- D. Boda, K.-Y. Chan, and D. Henderson, J.
Chem. Phys. 109, 7362 (1998).first
citation in article
- D. Boda, D. Henderson, and K.-Y. Chan, J.
Chem. Phys. 110, 5346 (1999).first
citation in article
- D. Boda, D. Henderson, K.-Y. Chan, and D. T.
Wasan, Chem. Phys. Lett. 308, 473 (1999) first citation in article
- L. Mier y Teran, D. Boda, D. Henderson, and S.
Quinones-Cisneros, Mol. Phys. 99, 1323 (2001). first citation in article
- D. Boda, D. Henderson, R. Rowley, and S. Soko
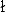 owski, J. Chem.
Phys. 111, 9382 (1999).first citation in
article
owski, J. Chem.
Phys. 111, 9382 (1999).first citation in
article
- D. Boda, D. Henderson, A. Patrkiejew, and S.
Soko
 owski, J.
Chem. Phys. 113, 802 (2000). first
citation in article
owski, J.
Chem. Phys. 113, 802 (2000). first
citation in article
- Y. Rosenfeld, J. Chem. Phys. 98, 8126
(1993). first citation in article
- D. Henderson, L. Blum, and J. L. Lebowitz, J.
Electroanal. Chem. 102, 315 (1979). first
citation in article
- W. Schmickler and D. Henderson, J. Chem. Phys. 80,
3381 (1984). first citation in article
- P. Linse, Macromolecules 29, 326 (1996).first citation in article
- See, for example, Fig. 19 of C. A. Barlow,
Jr., "The electric double layer," Physical Chemistry: An Advanced
Treatise, edited by H. Eyring (Academic, New York, 1970), Vol. IXA,
Chap. 2. first citation in article
- A. Hamelin, S. Rottgermann, and W. Schmickler,
J. Electroanal. Chem. 230, 281 (1987). first
citation in article
- R. Andreu and M. Molero, (unpublished). first citation in article
- W. Schmickler and D. Henderson, Prog. Surf.
Sci. 22, 323 (1986). first
citation in article
- J. N. Israelachvili, Intermolecular and
Surface Forces, 2nd Ed. (Academic, London, 1992), Fig. 13.10. first citation in article
- M. F. Toney, J. N. Howard, J. Richer, G. L.
Borges, J. G. Gordon, and O. R. Melroy, Surf. Sci. 335, 326
(1995) first citation in article
- D. Henderson and M. Lozada-Cassou, J. Colloid
Interface Sci. 114, 180 (1986). first
citation in article
- Z. Tang, L. E. Scriven, and H. T. Davis, J.
Chem. Phys. 97, 494 (1992). first
citation in article
- L. Zhang, H. T. Davis, and H. S. White, J.
Chem. Phys. 98, 5793 (1993). first citation in article
- Z. Tang, L. E. Scriven, and H. T. Davis, J.
Chem. Phys. 100, 4527 (1994). first citation in article
FIGURES
 Full figure (17
kB)
Full figure (17
kB)
Fig. 1. Electric potential at contact [part (a)] and
diffuse layer potential [part (b)] of a 1:1 electrolyte (d
= 3 Å) as a function of the electrode charge density.
The three sets of curves are, from top to bottom, for 0.01,
0.1, and 1 M. The points give the simulation results and the
solid and dotted-dashed curves give the DFT and PB/GC
results, respectively. First citation in article
 Full figure (17
kB)
Full figure (17
kB)
Fig. 2. Concentration profiles for a 1:1 electrolyte (d
= 3 Å) at 1 M for the state with the MC value of  *=0.1685
and
*=0.1685
and 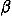 e
e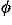 (d/2) =
2.60. The points give the simulation results and the solid
and dotted-dashed curves give the DFT and PB/GC results,
respectively. The comparison is made at the same electrode
charge density [part (a)] and at the same diffuse layer
potential [part (b)]. First citation in article
(d/2) =
2.60. The points give the simulation results and the solid
and dotted-dashed curves give the DFT and PB/GC results,
respectively. The comparison is made at the same electrode
charge density [part (a)] and at the same diffuse layer
potential [part (b)]. First citation in article
 Full figure (20
kB)
Full figure (20
kB)
Fig. 3. Electric potential at contact [part (a)] and
diffuse layer potential [part (b)] of a 2:1 electrolyte (d
= 3 Å) as a function of the electrode charge density.
The points are curves have the same meaning as in Fig. 1. First citation in article
 Full figure (17
kB)
Full figure (17
kB)
Fig. 4. Concentration profiles for a 2:1 electrolyte (d = 3
Å) at 1 M for the state with the MC value of *=-0.1685
and
*=-0.1685
and 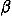 e
e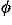 (d/2) =
-0.15. The points and curves have the same meaning as in
Fig. 2. The comparison is made at the
same electrode charge density [part (a)] and at the same
diffuse layer potential [part (b)]. First
citation in article
(d/2) =
-0.15. The points and curves have the same meaning as in
Fig. 2. The comparison is made at the
same electrode charge density [part (a)] and at the same
diffuse layer potential [part (b)]. First
citation in article
TABLES
Table I. The potential of
the electrode, 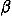 e e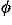 (0), for concentrations 0.1, 1, and 2 M,
for various electrode charges, for 1:1 and 2:1 electrolytes using
the ionic diameter d = 3 Å. (0), for concentrations 0.1, 1, and 2 M,
for various electrode charges, for 1:1 and 2:1 electrolytes using
the ionic diameter d = 3 Å. |
1:1
c (M) |
 * * |
| 0.0562 |
0.1123 |
0.1685 |
0.2247 |
| 0.1 |
4.01 |
5.85 |
7.21 |
8.43 |
| 1.0 |
2.21 |
3.81 |
5.12 |
6.32 |
| 2.0 |
1.73 |
3.19 |
4.49 |
5.64 |
2:1
c (M) |
 * * |
| 0.0562 |
0.1123 |
0.1685 |
0.2247 |
| 0.1 |
3.53 |
5.36 |
6.76 |
7.95 |
| 1.0 |
1.73 |
3.34 |
4.65 |
5.88 |
| 2.0 |
1.24 |
2.64 |
3.90 |
5.09 |
2:1
c (M) |
 * * |
| -0.0562 |
-0.1123 |
-0.1685 |
-0.2247 |
| 0.1 |
-1.99 |
-2.72 |
-3.32 |
-3.86 |
| 1.0 |
-1.35 |
-2.10 |
-2.67 |
-3.24 |
| 2.0 |
-1.20 |
-1.92 |
-2.48 |
-3.08 |
First citation in article
Table II. The diffuse layer
potential, 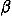 e e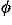 (d/2), for concentrations 0.1, 1,
and 2 M, for various electrode charges, for 1:1 and 2:1
electrolytes using the ionic diameter d = 3 Å. (d/2), for concentrations 0.1, 1,
and 2 M, for various electrode charges, for 1:1 and 2:1
electrolytes using the ionic diameter d = 3 Å. |
1:1
c (M) |
 * * |
| 0.0562 |
0.1123 |
0.1685 |
0.2247 |
| 0.1 |
3.17 |
4.16 |
4.69 |
5.07 |
| 1.0 |
1.37 |
2.13 |
2.60 |
2.96 |
| 2.0 |
0.89 |
1.51 |
1.97 |
2.28 |
2:1
c (M) |
 * * |
| 0.0562 |
0.1123 |
0.1685 |
0.2247 |
| 0.1 |
2.69 |
3.68 |
4.23 |
4.59 |
| 1.0 |
0.89 |
1.66 |
2.13 |
2.52 |
| 2.0 |
0.40 |
0.96 |
1.38 |
1.72 |
2:1
c (M) |
 * * |
| -0.0562 |
-0.1123 |
-0.1685 |
-0.2247 |
| 0.1 |
-1.15 |
-1.04 |
-0.80 |
-0.49 |
| 1.0 |
-0.51 |
-0.42 |
-0.15 |
0.12 |
| 2.0 |
-0.36 |
-0.24 |
0.05 |
0.28 |
First citation in article
FOOTNOTES
aCorresponding author. Electronic mail:
doug@huey.byu.edu
1
![[barred lower-case ell]](lstrok.gif) owski
owski , is equal to that
of the solvent, together with the combination of Poisson's equation,
, is equal to that
of the solvent, together with the combination of Poisson's equation,
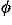 (r) is the electrostatic potential
at a distance r from a central ion, e is the
magnitude of the electronic charge, zi
and
(r) is the electrostatic potential
at a distance r from a central ion, e is the
magnitude of the electronic charge, zi
and 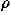 i
= Ni/V are the valence, including sign, and
number density of an ion of species i, and
i
= Ni/V are the valence, including sign, and
number density of an ion of species i, and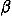 = 1/kT, k,
being the Boltzmann constant. The function gi(r)
is the normalized local density of an ion of species i at
a distance r from a central ion. The quantities, V,T,
and Ni are the volume, temperature, and number of
ions of species i, respectively. Gaussian (cgs) units are employed.
The difference in the formulas if rationalized MKS units are
used is slight.
= 1/kT, k,
being the Boltzmann constant. The function gi(r)
is the normalized local density of an ion of species i at
a distance r from a central ion. The quantities, V,T,
and Ni are the volume, temperature, and number of
ions of species i, respectively. Gaussian (cgs) units are employed.
The difference in the formulas if rationalized MKS units are
used is slight. 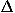
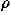 i(r)
=
i(r)
= 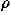 i(r)-
i(r)-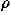 i,
of the inhomogeneous density from the uniform reference
density, yielding, after minimization of the free energy, an integral
equation that is somewhat similar in form to less successful
integral equations, such as the hypernetted chain (HNC) approximation equation.
As is common with integral equations for inhomogeneous fluids, the
DFT equation requires as input the direct correlation function (dcf)
of the uniform fluid. Because DFT is quite standard, we
refer to the paper of Rosenfeld18 for details. Why DFT
should be more accurate than say the HNC theory even when
the density inhomogeneities are very large as is the case
here, is far from clear. Certainly, the use of a nonlocal
density is crucial. Anyway, one cannot argue with success.
i,
of the inhomogeneous density from the uniform reference
density, yielding, after minimization of the free energy, an integral
equation that is somewhat similar in form to less successful
integral equations, such as the hypernetted chain (HNC) approximation equation.
As is common with integral equations for inhomogeneous fluids, the
DFT equation requires as input the direct correlation function (dcf)
of the uniform fluid. Because DFT is quite standard, we
refer to the paper of Rosenfeld18 for details. Why DFT
should be more accurate than say the HNC theory even when
the density inhomogeneities are very large as is the case
here, is far from clear. Certainly, the use of a nonlocal
density is crucial. Anyway, one cannot argue with success. 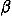 zizje2/
zizje2/ d =
2.3811zizj, or, equivalently, the
dimensionless temperature, T* =
d =
2.3811zizj, or, equivalently, the
dimensionless temperature, T* =  dkT/e2
= 0.419 95. Our earlier studies have shown that the smaller
the value of T*, or the larger the value
of the coupling constant, the greater the errors in the
PB/GC theory. Since a large coupling constant can be achieved
by reducing the temperature, the dielectric constant, or value ofd,
the value that is used here for d is likely to yield
more interesting results than that used by TV. If the reader
prefers rationalized MKS units, the definition of the
dimensionless coupling constant is
dkT/e2
= 0.419 95. Our earlier studies have shown that the smaller
the value of T*, or the larger the value
of the coupling constant, the greater the errors in the
PB/GC theory. Since a large coupling constant can be achieved
by reducing the temperature, the dielectric constant, or value ofd,
the value that is used here for d is likely to yield
more interesting results than that used by TV. If the reader
prefers rationalized MKS units, the definition of the
dimensionless coupling constant is 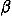 zizje2/4
zizje2/4
 0
0 d and the dimensionless
temperature is T* = 4
d and the dimensionless
temperature is T* = 4
 0
0 dkT/e2.
The numerical values of these dimensionless quantities is the
same in both systems of units.
dkT/e2.
The numerical values of these dimensionless quantities is the
same in both systems of units.
 is the charge per unit area on the electrode
surface. That is, the charge in the double layer must be the
negative of that of the electrode. All acceptable theories,
including PB/GC, satisfy this condition. As a result, we
will not emphasize this test. The second is the contact
value condition of Henderson et al.,19
is the charge per unit area on the electrode
surface. That is, the charge in the double layer must be the
negative of that of the electrode. All acceptable theories,
including PB/GC, satisfy this condition. As a result, we
will not emphasize this test. The second is the contact
value condition of Henderson et al.,19 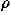 i(t)
=
i(t)
= 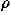 igi(t)
and p is the pressure of the bulk electrolyte. This
contact value condition is a force balance condition. The
momentum transfer at the electrode must equal p plus
the Maxwell stress. The corresponding PB/GC result is
igi(t)
and p is the pressure of the bulk electrolyte. This
contact value condition is a force balance condition. The
momentum transfer at the electrode must equal p plus
the Maxwell stress. The corresponding PB/GC result is 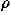 kT, and the
inverse compressibility are nearly equal in the PM for the
conditions considered here. Differences would be apparent
when a molecular solvent is considered, at molten salt
densities, or at low effective temperatures (or, equivalently, high coupling
constants).
kT, and the
inverse compressibility are nearly equal in the PM for the
conditions considered here. Differences would be apparent
when a molecular solvent is considered, at molten salt
densities, or at low effective temperatures (or, equivalently, high coupling
constants). 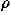 =
= ![[summation]](sum.gif)
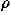 i.
Equation (8) is equivalent to Eq. (5) only if the relation between
i.
Equation (8) is equivalent to Eq. (5) only if the relation between  and
and 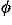 (d/2) that
is given by the PB/GC theory is accurate. If this relation
is not accurate, we know from the contact value theorem and
Eq. (5) that it is better to use charge
rather than potential as the variable. However, from the
point of view of logic there is no reason to make this
choice. In fact, within the PB/GC theory, the potential
seems more logical variable since it is the potential that
appears in the formulation of the PB/GC theory, Eq. (2), and many of the results of this theory,
especially for asymmetric electrolytes, are expressed more compactly if
the potential is used as the variable. In this paper, the
PB/GC theory and the DFT will be tested using both the
charge and potential as the variable that specifies the
system.
(d/2) that
is given by the PB/GC theory is accurate. If this relation
is not accurate, we know from the contact value theorem and
Eq. (5) that it is better to use charge
rather than potential as the variable. However, from the
point of view of logic there is no reason to make this
choice. In fact, within the PB/GC theory, the potential
seems more logical variable since it is the potential that
appears in the formulation of the PB/GC theory, Eq. (2), and many of the results of this theory,
especially for asymmetric electrolytes, are expressed more compactly if
the potential is used as the variable. In this paper, the
PB/GC theory and the DFT will be tested using both the
charge and potential as the variable that specifies the
system.  *=0.0562. A
concentration of 1 M is equal to a dimensionless density
of
*=0.0562. A
concentration of 1 M is equal to a dimensionless density
of 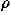 *=0.0162,
for the least abundant species. The PB/GC and DFT results
for these quantities for a 1:1 electrolyte are compared with
these MC results in Fig. 1 with parts (a) and (b)
giving the potential of the electrode,
*=0.0162,
for the least abundant species. The PB/GC and DFT results
for these quantities for a 1:1 electrolyte are compared with
these MC results in Fig. 1 with parts (a) and (b)
giving the potential of the electrode,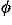 (0), and the diffuse layer potential,
(0), and the diffuse layer potential, 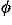 (d/2),
respectively, as functions of
(d/2),
respectively, as functions of  . The PB/GC potentials are
uniformly too large. On the other hand, the DFT results are
quite good. A comparison of the PB/GC and DFT profiles with
the MC results for a 1:1 electrolyte is given in Fig. 2, with
parts (a) and (b) making the comparison for the same
electrode charge and the same diffuse layer potential, respectively. The
PB/GC theory is somewhat better when the comparison is made
at the same electrode charge, but even then the PB/GC results
are still unsatisfactory. No matter what method is used for
the comparison, the DFT theory is in quite good agreement
with the MC results. These results are similar to those
reported for 1:1 electrolytes for d = 4.25 Å by TV, who
made comparisons of the profiles only for equal electrode charge.
In the TV simulations, the potential for a 1:1 electrolyte
rises strongly at (unphysically) large electrode charge densities and crosses
the PB/GC results, giving the illusion that the PB/GC theory
is not so bad. However, the MC counterion profile contains a
second layer.12 This is seen in DFT,19 but not in the PB/GC theory.
Presumably, a second layer would also be seen at large
charge densities with the MC and DFT techniques for the
system considered here. We do not pursue this question since
unphysically large charges and potentials are involved.
. The PB/GC potentials are
uniformly too large. On the other hand, the DFT results are
quite good. A comparison of the PB/GC and DFT profiles with
the MC results for a 1:1 electrolyte is given in Fig. 2, with
parts (a) and (b) making the comparison for the same
electrode charge and the same diffuse layer potential, respectively. The
PB/GC theory is somewhat better when the comparison is made
at the same electrode charge, but even then the PB/GC results
are still unsatisfactory. No matter what method is used for
the comparison, the DFT theory is in quite good agreement
with the MC results. These results are similar to those
reported for 1:1 electrolytes for d = 4.25 Å by TV, who
made comparisons of the profiles only for equal electrode charge.
In the TV simulations, the potential for a 1:1 electrolyte
rises strongly at (unphysically) large electrode charge densities and crosses
the PB/GC results, giving the illusion that the PB/GC theory
is not so bad. However, the MC counterion profile contains a
second layer.12 This is seen in DFT,19 but not in the PB/GC theory.
Presumably, a second layer would also be seen at large
charge densities with the MC and DFT techniques for the
system considered here. We do not pursue this question since
unphysically large charges and potentials are involved.  Figure
1.
Figure
1.  Figure
2.
Figure
2.
 Figure
3.
Figure
3.  Figure
4.
Figure
4.  owski, J. Chem.
Phys. 111, 9382 (1999).first citation in
article
owski, J. Chem.
Phys. 111, 9382 (1999).first citation in
article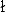 owski, J.
Chem. Phys. 113, 802 (2000). first
citation in article
owski, J.
Chem. Phys. 113, 802 (2000). first
citation in article Full figure (17
kB)
Full figure (17
kB)
 Full figure (17
kB)
Full figure (17
kB)  *=0.1685
and
*=0.1685
and 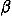 e
e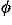 (d/2) =
2.60. The points give the simulation results and the solid
and dotted-dashed curves give the DFT and PB/GC results,
respectively. The comparison is made at the same electrode
charge density [part (a)] and at the same diffuse layer
potential [part (b)]. First citation in article
(d/2) =
2.60. The points give the simulation results and the solid
and dotted-dashed curves give the DFT and PB/GC results,
respectively. The comparison is made at the same electrode
charge density [part (a)] and at the same diffuse layer
potential [part (b)]. First citation in article
 Full figure (20
kB)
Full figure (20
kB)  Full figure (17
kB)
Full figure (17
kB)  *=-0.1685
and
*=-0.1685
and 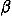 e
e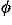 (d/2) =
-0.15. The points and curves have the same meaning as in
Fig. 2. The comparison is made at the
same electrode charge density [part (a)] and at the same
diffuse layer potential [part (b)]. First
citation in article
(d/2) =
-0.15. The points and curves have the same meaning as in
Fig. 2. The comparison is made at the
same electrode charge density [part (a)] and at the same
diffuse layer potential [part (b)]. First
citation in article 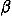 e
e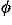 (0), for concentrations 0.1, 1, and 2 M,
for various electrode charges, for 1:1 and 2:1 electrolytes using
the ionic diameter d = 3 Å.
(0), for concentrations 0.1, 1, and 2 M,
for various electrode charges, for 1:1 and 2:1 electrolytes using
the ionic diameter d = 3 Å.  *
* *
* *
*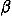 e
e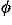 (d/2), for concentrations 0.1, 1,
and 2 M, for various electrode charges, for 1:1 and 2:1
electrolytes using the ionic diameter d = 3 Å.
(d/2), for concentrations 0.1, 1,
and 2 M, for various electrode charges, for 1:1 and 2:1
electrolytes using the ionic diameter d = 3 Å.  *
* *
* *
*