Az
intermolekuláris kölcsönhatások áttekintése
Az
előző fejezetben vázoltuk azokat a statisztikus mechanikai alapokat, amelyek
révén egy termodinamikai rendszert jellemző konfigurációs mennyiségek
meghatározhatók. Ha a termodinamikai határfeltételeket rögzítettük,
"csupán" az intermolekuláris párpotenciált kell ismernünk. Ennek
meghatározása meglehetősen nehéz feladat.
Két
alapvető osztályát ismerjük az intermolekuláris potenciáloknak. Az egyik
esetben ab initio kvantummechanikai számításokat végeznek az egymáshoz képest 
helyzetben lévő
különálló párok nagy számú konfigurációjára, és a kapott eredményekhez
analitikus függvényeket illesztenek. Az alkalmazott közelítésektől függően
(bázis nagysága, korrelációs energia figyelembevétele stb.) ez nagyon
számolásigényes feladat.
Ezért
gyakran teljesen empirikus modellpotenciálokat használnak. Ezek olyan
analitikus egyenletek, melyek általában több, a kölcsönhatásban részt vevő
molekulákra jellemző paramétert tartalmaznak. A paramétereket úgy határozzák
meg, hogy a modellből számolt elméleti eredmények illeszkedjenek a kísérleti
adatokhoz. Általában spektroszkópiai- és molekulasugár-kísérletekből, illetve a
modell-paraméterek transzport- és termodinamikai (fázisegyensúlyi)
tulajdonságokhoz való illesztéséből szerezhetünk információkat. Sokszor a két
módszer (empirikus, ab initio) kombinálásával állítják elő a megfelelő
potenciált.
Minél
bonyolultabb, több paramétert tartalmazó a modellpotenciál, annál pontosabban
írható le az illető fluidum; ekkor azonban a számítási munka is
megsokszorozódik. Kompromisszumot kell kötni a valóság pontos leírása és a
kezelhetőség között. Már meglehetősen bonyolult molekulákból álló fluidumokra
is (úgymint alkánokra, alkoholokra, éterekre, asszociált folyadékokra stb.)
határoztak meg realisztikus intermolekuláris potenciálokat és végeztek
szimulációkat. Rendkívül kiterjedt a vízre vonatkozó irodalom.
Általában
olyan modellpotenciálokat használunk, melyek kevés paramétert tartalmaznak,
könnyen kezelhetők, ezért az irodalomban is rendkívül elterjedtek. Ezáltal mód
nyílik eredményeinknek más szerzők eredményeivel való összehasonlítására. A
rendelkezésünkre álló számítástechnikai kapacitás szűkös
Feltehető,
hogy a párpotenciál a tömegközéppontok távolságától függ. Szokás a
párpotenciált különböző járulékok összegére bontani:
(1) Rövid hatótávolságú
vegyérték- vagy kémiai energiák. Kémiailag telített molekulák (csak ilyeneket
vizsgálunk) esetében ez pozitív járulék, taszító erőnek felel meg, és az
elektronfelhők átfedésekor fellépő kvantummechanikai kizárási-elv
következménye. Ezek a potenciálok jól közelíthetők a következő exponenciális
kifejezéssel: 
. Egy adott intervallumon ez a 
függvénnyel
helyettesíthető, amely intervallumon s jó közelítéssel konstansnak vehető.
További egyszerűsítés az, hogy ha s-et
az egész intervallumon állandónak tekintjük.
(2) Rövid vagy közepes
hatótávolságúak az átmeneti jellegű kölcsönhatások, melyekre példa a
hidrogénkötés és a töltésátviteli kölcsönhatások. A kémiai kötés energiájánál
kisebb energiájúak (0.05-0.5 eV) és ún. asszociált molekulákat hoznak létre.
Ezek tárgyalása meglehetősen bonyolult és nem képezi jelen dolgozat tárgyát.
(3) A van der Waals erők akkor
lépnek fel, amikor a molekulák olyan messzire kerülnek egymástól, hogy
elektronfelhőik nem lapolódnak át. Gyenge, vonzó jellegű kölcsönhatások, ezek
okozzák a gázok ideális állapottól való eltérését, ill. a molekulakristályok
kohézióját. Kvantummechanikai tárgyalásuk perturbációszámítással történik. A
perturbációs sorfejtésben a következő járulékok lépnek fel:
(a) Amennyiben a
kölcsönhatásban résztvevő molekuláknak állandó elektromos (dipólus, kvadrupólus
stb.) nyomatékuk van, azaz a molekula nem gömbszimmetrikus, a közvetlen
elektrosztatikus kölcsönhatások lépnek fel. Ezek a klasszikus elektrosztatika
segítségével jól tárgyalhatók, a molekulát alkotó töltéseloszlásra a
multipólus-sorfejtést alkalmazva, a teljes kölcsönhatás a különböző elektromos
nyomatékok közötti kölcsönhatások összegeként áll elő (dipólus-dipólus,
dipólus-quadrupólus, quadrupólus-quadrupólus stb.). A dipólus-dipólus
kölcsönhatást a következő potenciállal írunk le (Gauss mértékegységrendszerben):
ahol 
az 
vektor irányába mutató
egységvektor. Reális gázok esetén a hőmozgás energiája nagyobb, mint 
, ekkor a molekulák a Boltzmann-eloszlás szerint állnak be a
különböző irányokba. A szögek szerinti átlagolás után (első rendben) a
dipólusirányítási vagy Keesom-féle kölcsönhatáshoz jutunk, amely a távolság
hatodik hatványával fordítottan arányos: 
.
Ha töltött
részecskét (iont) modellezünk, a Coulomb kölcsönhatást használjuk
(b) Az indukciós vagy
polarizációs energiák oka, hogy valamely molekula töltéseloszlása a másik
molekula permanens multipólusa által polarizálódik. Az indukált momentum
kölcsönhatásba lép a másik molekula permanens momentumával. Irány szerint
átlagolt alakja adja az ún. Debye-féle kölcsönhatást. Itt ezzel a
kölcsönhatással sem foglalkozunk.
(c) Míg az előző két
kölcsönhatás klasszikusan tárgyalható, az ingadozási vagy diszperziós energiák
csak a kvantumelméletből határozhatók meg. Bár az atomok és az apoláros
molekulák pozitív és negatív töltéseinek középpontja időátlagban egybeesik, a
töltéseloszlás gyorsan változik, emiatt gyorsan változó momentum jön létre, ami
kölcsönhatásba lép a másik részecske hasonló, pillanatnyi momentumával. Ez egy
vonzó kölcsönhatást eredményez, ami az elektronkorreláció következménye. Az
elektronok a korreláció miatt úgy helyezkednek el, hogy az összetett rendszer
energiája kisebb legyen. A számolásokat elvégezve a diszperziós potenciálra egy
az 
hatványai szerinti
aszimptotikus sort kapunk:
ahol a hatodrendű tagok a
dipólus-dipólus, a nyolcadrendűek a dipólus-kvadrupólus, a tizedrendűek a
dipólus-oktopólus és a kvadrupólus-kvadrupólus stb. kölcsönhatásoknak felelnek
meg. Az oszcillátormodellt alkalmazva, melyben a molekulák kvantumállapotait
harmonikus oszcillátorokkal modellezik, a fenti együtthatókra a molekulák
polarizálhatóságát, és ionizációs energiáját tartalmazó kifejezések vezethetők
le. Ezek az ún. London-Margenau-formulák.
Egy
adott molekulapár közötti összetett potenciál felépítésekor többféle módon
szoktak eljárni. Szokás a potenciált felosztani izotróp és anizotróp összetevőkre.
Az izotróp tag gömbszimmetrikus és tartalmazza a rövid távú taszító és a
diszperziós kölcsönhatást egyaránt. Az általános Buckingham-potenciál alakja: 
. Ezen különböző
közelítő jellegű egyszerűsítések hajthatók végre. Ha mind a diszperziós,
mind az exponenciális taszító tagot egy
hatványfüggvénnyel közelítjük, akkor a Mie-potenciálhoz jutunk: 
.
Az
egyszerű centrális potenciálokat szokás a következő, egy energia- és egy
távolságparamétert tartalmazó, formában felvenni: 
. A disszertációban előforduló potenciálok a következők. A
részecskét egy 
átmérőjű merev gömbnek
feltételezve a merevgömb (HS) potenciálról beszélünk:
A Mie-potenciál speciális esete a
rendkívül elterjedt 6,12 vagy Lennard-Jones potenciál:
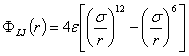
A diszperziós kölcsönhatást
elhanyagolva a taszító lágygömb (SS) potenciált kapjuk:
A csak taszító tagot tartalmazó merev-
és lágygömb potenciálok főként magas nyomáson ill. hőmérsékleten nyújtanak
elfogadható modellt a reális rendszerekre.
Az
anizotróp tag az indukciós és elektrosztatikus kölcsönhatásokat, valamint egy a
molekula alakjára jellemző tagot tartalmaz. Ez utóbbit gyakran írják le egy
szögfüggő, rövid hatótávolságú átlapolódási potenciállal, melyet
gömbharmonikusok szerint sorfejtett alakban vesznek fel. Megjegyezzük, hogy
egyes alkalmazásokban a teljes potenciált is így írják fel. A molekula
alakjának figyelembe vételére sokkal inkább elterjedt módszer a többcentrumú
potenciálok használata, ahol a molekulát több, általában az atomokon
elhelyezett, centrális, atomi potenciálokkal jellemzik (többcentrumú Lennard-Jones
modell).