A Monte Carlo módszer alapjai

A számítógépes szimulációs módszerek az anyagi rendszer mikroszkopikus tulajdonságainak, azaz a molekulák vagy atomok közötti kölcsönhatásoknak az ismeretében a sokrészecskés rendszer mikroállapotait közvetlenül modellezik és a fázistérből ily módon mintát véve a keresett tulajdonságokat sokaság- vagy időátlagként számítják. Az intermolekuláris potenciálokon kívül szükség van még néhány termodinamikai állapotjelző rögzítésére a használt sokaságtól függően. Két alapvető szimulációs módszer létezik, az egyik a molekuláris dinamikai (MD), a másik a Monte Carlo (MC) módszer. A MD szimulációk során a rendszer fázistérbeli trajektóriáját a klasszikus newtoni mozgásegyenletekkel határozzák meg. A trajektória mentén számított fizikai mennyiségek átlaga időátlagnak tekinthető MD szimulációk során.

A disszertációban a Monte Carlo módszert alkalmaztuk, ezért ezt részletesebben ismertetjük. A Monte Carlo szimulációk során véletlenszerűen veszünk mintát a konfigurációs tér pontjai közül, így különböző mikroállapotú rendszerek sokaságát állítjuk elő. A módszer nem alkalmas nemegyensúlyi, időben változó rendszerek vizsgálatára, csak az egyensúlyban levő rendszerek sztatikus jellemzői határozhatóak meg. A részecskék „mozgása” indeterminisztikus, valószínűségi törvénynek engedelmeskedik.

A módszer alapjait a kanonikus sokaságon ismertetjük. Tekintsünk egy V térfogatú, kocka alakú szimulációs cellát, amely N részecskét tartalmaz. Esetenként több százezres nagyságrendű részecskeszámmal is végeznek szimulációkat, de a minta még így sem tekinthető makroszkopikusnak. Az oka a következő: a szimulációs doboz határfelületén nagyon sok részecske helyezkedik el, így a határfelületi jelenségek szerepe jelentős. A periodikus határfeltétel alkalmazásával kiküszöbölhetőek a határfelületi jelenségekből származó hibák, mivel a középpontinak tekintett cella körül ebben az esetben végtelen számú ugyanolyan cella helyezkedik el. Ezekben a cellákban a szellemrészecskék ugyanúgy mozognak, mint a központi cella részecskéi. Ez azt jelenti, hogy ha egy részecske kilép a kockából egy adott irányban, a szomszéd cellából belép a megfelelő „szellemrészecske” az ellentétes irányból.

Valamely konfigurációs fizikai mennyiség értéke a

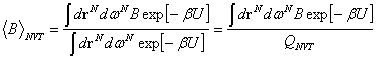
egyenlet szerint adott. A nevezőben a kanonikus konfigurációs integrál található. Az integrálok megbecsülhetőek úgy, hogy a konfigurációs tér elegendően sok pontjában kiszámítjuk és értékét, így az integrált összegzéssel helyettesítjük:

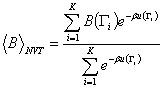
ahol K a mintapontok száma. A MC szimulációk során a teljes konfigurációs térből kell egyenletesen mintát venni majd azt a Boltzmann faktorral súlyozva figyelembe venni. Ez az eljárás még mindig meghaladja a számítógépek teljesítőképességét.

A számítási idő jelentősen csökkenthető, ha a mintát nem egyenletes eloszlás szerint vesszük, azaz ha egy adott pont valamely eloszlásnak megfelelő valószínűséggel kerül kiválasztásra. Az ilyen mintavétel során csak azokra a konfigurációs pontokra koncentrálunk, amelyek jelentős járulékot adnak az állapotösszeghez. A fenti átlagban a súlyozást kompenzálni kell, így:

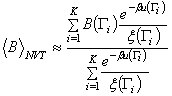
Ha a mintavételnél alkalmazott eloszlás a Boltzmann-eloszlás , akkor Boltzmann-mintavételről beszélünk, vagyis az átlagolásnál azonos súllyal vesszük figyelembe a számolt értékeket:

.

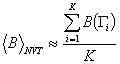A Metropolis féle mintavételezés lényege a következő. A mintapontokat Markov lánc tagjainak tekinti, ahol annak a valószínűsége, hogy bekerül a mintába csak a lánc előző tagjától függ. Ha és lehetséges állapotai a rendszernek és az ehhez tartozó Boltzmann faktorok és , akkor az i állapotból j-be való átmenet valószínűsége () egy sztochasztikus mátrixot definiál, amelyre a következő feltételek teljesülnek:

és minden i-re.

Egy adott kezdeti állapotból kiindulva a Markov folyamat segítségével állítjuk elő az egymás után következő állapotok sorozatát, amelyet a fenti átmeneti mátrix irányít. A mátrix sajátvektora a Boltzmann-eloszlás által meghatározott határeloszlás, amelynek sajátértéke egységnyi. Ehhez az ismert határeloszláshoz olyan átmeneti mátrixot kell találni, amely kielégíti a fenti feltételeket, valamint a mátrixelemek függetlenek az állapotösszegtől. Az említett feltételeket pl. a következő konstrukció elégíti ki:

Ezt nevezik a mikroszkopikus reverzibilitás feltételének is, és lényege az, hogy egyensúlyban a szimulációban az i állapotból a j-be jutás valószínűsége ugyanakkora, mint a j állapotból az i-be jutás valószínűsége. Az átmeneti valószínűség két tag szorzataként áll elő:

ahol a_ij annak valószínűsége, hogy a szimuláció során az i állapot után a j állapotot sorsoljuk, míg P_ij annak a valószínűsége, hogy az i állapotból a j állapotba való mozgatást elfogadjuk. Ha az a_ij mátrix szimmetrikus, mint a mi szimulációink esetében (nem feltétlenül kell szimmetrikusnak lennie), akkor írhatjuk, hogy:

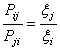
Metropolis és munkatársai a következő megoldást adták a problémára [57-60]:

Az mátrixra a következő algoritmust alkalmazhatjuk. Megpróbálunk a kocka belsejében egy véletlenszerűen kiválasztott részecskét véletlenszerűen elmozgatni. A részecske új helyét egy egyenletes eloszlást produkáló véletlenszám-generáló rutin segítségével sorsoljuk a következő módon:

ahol a (0,1) intervallumban egyenletesen generált véletlenszámok. Ez azt jelenti, hogy a részecskét egy a régi hely körüli 2Dr_max élhosszúságú kockán belül egy véletlenszerűen kiválasztott pontba áthelyezzük. Ha Dr_max kicsi, akkor a részecske új helye a régihez közel van. Ez különösen hasznos folyadékokban, valamint a polarizálható fluidumok esetében, ahol az indukált dipólusmomentumok újraszámolását végző iteratív rutin gyorsabban konvergál, ha az indukált dipólusmomentumok átrendeződését generáló változás, azaz a részecske elmozdulása kicsi. Ha a rendszer sűrűsége kicsi (gáz vagy híg oldat), a részecske új pozícióját sorsolhatjuk véletlenszerűen a teljes szimulációs cellában a régi pozíciótól teljesen függetlenül.

A Boltzmann-eloszlást helyettesítve helyébe akkor fogadjuk el az elmozdítást, ha az összenergia csökkent a folyamat során. Ha ez nem áll fenn, akkor az elmozdítás elfogadásának valószínűsége:

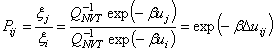
Látható, hogy az algoritmus szükségtelenné teszi az állapotösszeg kiszámítását. Ha az intermolekuláris potenciál nem gömbszimmetrikus, akkor a molekulák orientációját, azaz a polárszögeket is véletlenszerűen meg kell változtatni valamely határokon belül.

Egy részecske kölcsönhatási energiájának számításakor azon L élhosszúságú kockában levő részecskéket kell figyelembe venni, amelynek a középpontjában az adott részecske helyezkedik el. A részecske energiáját szférikus levágás alkalmazásával kapjuk meg, vagyis az r_c (ahol r_c általában L/2-vel egyenlő) sugarú gömbön belül levő részecskékkel vett párkölcsönhatási energiákat összegezzük, míg a fennmaradó, gömbön kívül eső részecskék hatását hosszútávú korrekciókkal vesszük figyelembe. Ennek számítására a rövid hatótávolságú potenciálok (mint például a LJ potenciál) esetén pontos közelítő módszer áll rendelkezésünkre. Feltételezzük, hogy a párkorrelációs függvény egységnyi a központi részecskétől r_c-től nagyobb távolságban, így az energia hosszútávú korrekciója (LRC, Long Range Correction) a következő módon számítható:

.

Lennard-Jones potenciál esetén az integrálást elvégezve:

.

Dipólus-dipólus kölcsönhatás esetén a potenciál hosszú hatótávolságú és irányfüggő. A hosszútávú korrekciók kezelésére többféle módszert választhatunk. A két legfontosabb a reakciótér [61] és az Ewald-Kornfeld összegzési módszerek [62].

A reakciótér módszer (amit a dolgozatban használunk) lényege a következő [61]. Az r_c sugarú gömb középpontjában levő dipólus energiájának számításakor a gömbön kívül levő dipólusokat egy e_RF dielektromos állandójú folytonos közeggé „mossuk össze”, és a központi dipólusnak ezekkel való kölcsönhatását, azaz a hosszú távú korrekciót a dipólus és a reakciótér kölcsönhatásaként közelítjük. A reakciótér a gömbben levő összes dipólus által a minta és az azt körülvevő dielektrikum határfelületén indukált polarizációs töltések által kifejtett erő. Erről részletesebben a 2.3 fejezetben volt szó, a reakciótérrel való kölcsönhatást a következő egyenlet definiálja:

,

ahol M az sugarú mintában (melynek középpontjában a dipólus helyezkedik el) levő összes dipólusmomentum.

Ahogy azt a 2.3 fejezetben kifejtettük, a határfeltételtől, azaz –től függ a reakciótér, a dielektromos állandó és a Kirkwood-faktor közti kapcsolat, külső tér alkalmazása esetén a létrejövő polarizáció is. Ugyanakkor függetlenek az alkalmazott határfeltételtől az állapotfüggvények és a dielektromos állandó is.

Az Ewald-Kornfeld szummázás [62] során kiszámítják a részecske kölcsönhatási energiáját az összes többi, szomszédos dobozban elhelyezkedő szellemrészecskével. Ez az összegzés is csak véges rendszerre végezhető azonban el és a (nagyobb) rendszert szintén dielektrikum veszi körül: ekkor fellép egy ún. felületi tag, de az ebből származó hiba az esetek többségében elhanyagolható.