Ioncsatornák szelektivitásának Monte Carlo szimulációs vizsgálata*

Letölthető WinWord doc formátumban
 

Boda Dezső

Fizikai Kémia Tanszék, Veszprémi Egyetem, 8201 Veszprém, Pf:. 158

 

Bevezető

 

       Az ioncsatornák az ionoknak a sejtmembránon keresztül való transzportját szelektív módon megvalósító fehérjék. Ezen közlemény célja, hogy egy statisztikus termodinamikai leírásmód és Monte Carlo szimulációk, mint metodika segítségével megvizsgálja, hogy az ioncsatornák szerkezete milyen módon határozza meg azok ionszelektivitását. Egy rövid, az ioncsatornák élettani jelentőségét és szerkezetét bemutató áttekintés után közöljük a kalcium- és nátriumcsatornák szelektivitására vonatkozó eredményeinket.

 

Molekuláris biológiai háttér

 

A sejtet határoló lipid kettősréteg, azon túl, hogy definiálja a sejt határait, védi azt a külső behatásoktól és mechanikai stabilitást biztosít neki. A középen elhelyezkedő hidrofób réteg révén az ionokra és nagyobb poláros molekulákra ez a lipidréteg nem áteresztő. Ahhoz, hogy élő sejtről beszélhessünk, szükség van a sejt és környezete kölcsönhatására: információcserére, anyagtransz-portra. Az olyan részecskék transzportjára, amelyeket a lipidréteg nem ereszt át, a természet ún. membránfehérjéket alkotott. Ezek a lipidrétegen keresztültüremkedő óriásmolekulák felelősek sok más funkció mellett a különböző fiziológiailag fontos szervetlen ionok (Na+, K+, Ca++, Cl-) sejtmembránon keresztül való transzportjáért.

Szigorúan véve a sejtmembránt a lipidréteg és a membránfehérjék együtteseként definiálják. A sejtmembrán tömegének mintegy 50%-át a membránfehérjék teszik ki. A részecskék továbbítására szolgáló fehérjéket több szempont szerint lehet csoportosítani. Aszerint, hogy az illető komponens továbbítása annak elektrokémiai gradiense mentén, vagy azzal szemben történik, passzív vagy aktív transzportról beszélünk. Aktív transzport során kémiai vagy fényenergia, illetve egy másik komponens passzív transzportjának felhasználásával (csatolt transzport) történik a továbbítás.

Passzív transzport esetén, és ide tartoznak az ioncsatornák is, a membrán két oldala közt az adott komponensre vonatkozó koncentrációgradiens, illetve a potenciálkülönbség (ionok esetében) együttes hatására mozognak a részecskék. Ezt a jelenséget szokás elektrodiffúziónak nevezni és a Nernst-Planck egyenlet írja le. A sejten belül (citoplazma) és kívül a különböző ionoknak eltérő a koncentrációja (ld. 1. Táblázat). Ezeket a koncentrációgradienseket az aktív pumpák (mint pl. a Na+-K+ pumpa) tartják fenn. Látható, hogy pl. a kálium-ionoknak a sejten belül sokkal nagyobb a koncentrációja, mint azon kívül. Ehhez a koncentráció-arányhoz a Nernst-egyenlet szerint egy kb. –100 mV-os potenciálkülönbség tartozik. Mivel egy tipikus állati sejtben, nyugalmi állapotban a sejtmembrán, az ún. szivárogtató káliumcsatornák révén a káliumionokra nézve permeábilis, az egyensúlyi membránpotenciált ezek határozzák meg.

 

1. táblázat

 

A különböző, fontosabb ionok koncentrációja a sejten belül és kívül egy tipikus állati sejtben.

 

Koncentráció (mM)

Belül

Kívül

Kationok

 

 

Na+

5-15

145

K+

140

5

Ca++

10-7

1-2

Anionok

 

 

Cl-

5-15

110

Szerves molekulák

Magas

0

 

Az ioncsatornáknak két nagyon fontos tulajdonságát kell megemlítenünk. Az egyik, hogy erősen szelektívek, azaz csak egyfajta ionra nézve áteresztőek, míg a többi ionra nézve inkább nem. Ez természetesen egy valószínűségi kijelentés, ami azt mondja, hogy a csatorna azt az iont, amelyre szelektív, nagyobb valószínűséggel engedi át, mint a többit. Jelen közlemény ennek a jelenségnek a vizsgálatával foglalkozik. Jelesül, arra a kérdésre szeretnénk választ kapni, hogy hogyan következik a fehérje struktúrális tulajdonságaiból a csatorna szelektivitása.

Szelektivitásról természetesen csak nyitott csatorna esetében van értelme beszélni, és ez az ioncsatornák másik alapvető jellemzője: nyitott vagy zárt állapotban lehetnek, mégpedig szabályozott módon (gating). A nyitott illetve zárt állapot a fehérje kétféle konformációját jelenti. A membrán nyugalmi állapotában a legtöbb csatorna zárt állapotban tartózkodik. (Kivételt képeznek pl. a fent említett káliumcsatornák.) Ahhoz, hogy a csatorna kinyisson, valamilyen inger szükséges. Ez lehet egy kémiai jel, amikor valamilyen hírvivő molekula (ligandum) kötődik a fehérjéhez. Lehet mechanikai behatás, mint pl. a hallósejtekben.

Jelen dolgozat szempontjából a feszültség-vezérelt (voltage gated) ioncsatornák képezik a legfontosabb csoportot, mivel ide tartoznak az itt vizsgált kalcium- és nátriumcsatornák. Itt egy elektromos ingerület, az ún. akciós potenciál hatására nyit a csatorna. Ez az akciós potenciál nem más, mint a membránpotenciál hirtelen megváltozása.

Ezen a helyen szükséges annak rövid ismertetése, hogy mi a jelentősége a kalcium és nátrium-csatornáknak az idegrendszer működésében. Sok egyéb funkció mellett ezek az ioncsatornák itt játsszák a legfontosabb és legszemléletesebb szerepet. A nátriumcsatornáknak az ingerületnek az idegrost (axon) mentén való továbbításában van nélkülözhetetlen szerepe. Ehhez azt kell látni, hogy hogyan keletkezik az akciós potenciál. Ha a sejt-membrán egy adott részére elektromos inger érkezik, azaz megváltozik a membránpotenciál, az ott levő nátriumcsatornák kinyitnak (valójában ez is egy valószínűségi kijelentés: nagyobb valószínűséggel tartózkodnak nyitott állapotban). Mivel a nátriumionoknak a sejten kívül sokkal nagyobb a koncentrációja (ld. 1. táblázat), és erre a negatív nyugalmi membránpotenciál csak „rásegít”, egy nagy befelé mutató elektrokémiai gradiens érvényesül a nátriumionokat illetően, ami egy nagy nátriumion-fluxust eredményez. Ez az áram viszont megváltoztatja a nátriumionok koncentráció-arányát a membránnak a nyitott nátriumcsatornák melletti részén, és ezzel együtt a membrán-potenciált is. Ez a potenciálváltozás viszont nyitja az ott lévő nátriumcsatornákat. Ez a ciklus az alapja annak a folyamatnak, melynek során az elektromos ingerület a membrán felületén, azaz az idegrost mentén továbbterjed, mégpedig gyengítetlenül. A gyengítetlen tovaterjedéshez szükséges energiát a Na+-K+ pumpák által fenntartott Na+ és K+-koncentrációgradiens biztosítja végeredményben kémiai energia (ATP) felhasználásával.

A kalciumcsatornák akkor lépnek be a képbe, amikor az inger az idegvégződéshez ér. Ekkor az elektromos inger hatására a feszültségvezérelt kalciumcsatornák kinyitnak az idegvégződésnél, avagy szinapszisnál, az idegvégződésbe áramló kalciumionok az ún. szinaptikus vezikulákban tárolt hírvivő molekulák, a neurotranszmitterek felszabadulását okozzák. Ily módon az elektromos ingerület kémiai ingerületté alakul át. A kémiai ingerület a neurotranszmitter-vezérelt ioncsatornák nyitásával alakul vissza elektromos ingerületté.

 

Az ioncsatornák szerkezete

 

A membránfehérjék pontos szerkezetéről a tudásunk korlátozott. Egy fehérjemolekula szerkezetét az őt felépítő aminosavak sorrendje határozza meg. Ezt az aminosavszekvenciát viszonylag nagy (sok aminosavból álló) fehérjék esetében is meg tudták határozni, annak visszafejtése azonban, hogy a polipeptid lánc miféle háromdimenziós szerkezetbe fog feltekeredni, csak viszonylag kicsi fehérjék esetében lehetséges. A membránfehérjék azonban többnyire igen nagy molekulák.

A fehérjék szerkezetének meghatározására használt legfőbb közvetlen módszer a röntgendiffrakció. Ehhez azonban, és ebben rejlik a fő nehézség, először kristályosítani kell az adott fehérje-molekulát. Ez nem könnyű feladat. A membrán-fehérjék esetében kiváltképp nem az, mivel ezek a fehérjék egy speciális környezetben helyezkednek el, középső részüket a lipid kettősréteg hidrofób része veszi körül, míg a két végük vizes közegben helyezkedik el. Tisztán vizes oldatban a fehérje más konformációba tekeredhet fel. Erről tanúskodik az, hogy míg összesen több mint ezer fehérje szerkeze-tét sikerült megmérni, az ismert konformációjú membránfehérjék száma csupán néhány tucat.

Direkt és indirekt módszerek segítségével azonban viszonylag átfogó képpel rendelkezünk az ioncsatornák szerkezetéről. Ezek a fehérjék ún. a-hélix kötegek formájában járják keresztül a membránt, kialakítva így egy hidrofil pórust, ami az ionok transzportját lehetővé teszi. A KcsA bakteriális feszültségvezérelt káliumcsatorna azon kevés ioncsatornák közé tartozik, amelyek szerkezetét röntgendiffrakciós mérésekből ismerjük (Roderick MacKinnon nem véletlenül kapott kémiai Nobel díjat4). A csatorna átfogó szerkezete az 1. Ábrán látható. Úgy tartják, hogy a lényeget tekintve a kalciumcsatornák és nátriumcsatornák szerkezete ehhez nagyon hasonló. Az egyik fő különbség, hogy míg a K csatornánál a négy -hélix négy különálló fehérjéhez tartozik, addig a Na és Ca csatornáknál azok egy fehérje alegységei. A másik fő különbség egy a póruson belüli szűk térrész, a szelektivitást meghatározó szelektív szűrő szerkezetében rejlik.



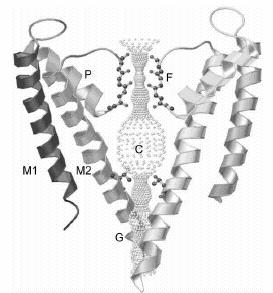
1.       ábra

 

A KcsA bakteriális káliumcsatorna vázlatos szerkezete. A szűrő (F) a sejten kívüli oldalon helyezkedik el és a P-spirálhoz tartozó polipeptid láncok határolják. A kapu (G) a sejten belüli oldalon helyezkedik el, középen egy hidrofil üreg (C) található3.

 

A KcsA csatorna esetében a szűrőt a polipeptid vázhoz tartozó oxigénatomok határolják, és az oldalláncok kifele állnak. Ezzel szemben a nátrium- és kalciumcsatornák esetében az aminosav oldal-láncok befele állnak, és az ioncsatorna szelektivitását éppen az határozza meg, hogy a szelektív szűrőt miféle aminosav oldalláncok határolják. A kalciumcsatornák esetében ezek az oldalláncok glutaminsavak (jelük: E), mégpedig négy darab (EEEE-locus). Ezek végén karboxilcsoportok helyezkednek el, általában deprotonált formában. A szelektív szűrőben így –4e töltés van jelen, ami a csatornát kationszelektívvé teszi. A szelektív szűrő kis térfo-gata teszi a csatornát kalciumszelektívvé, mivel a kalciumionok kétszer akkora töltést szolgáltatnak a töltött karboxilcsoportok semlegesítésére, mint a nátriumionok, miközben nagyjából ugyanakkora térfogatot foglalnak el. Ez a mechanizmus egyszerű fiziko-kémiai elvekkel magyarázza a csatorna kalci-umszelektivitását5. Jelen dolgozat célja, hogy az ioncsatorna egy egyszerű, de jól definiált modelljére végrehajtott Monte Carlo szimulációk segítségével igazolja, hogy a fent leírt mechanizmus (melyet, magyarra meglehetősen nehezen lefordíthatóan, ‘charge-space competition’ mechanizmusának neveztünk el) képes az ionszelektivitás magyarázatára.

Ami a nátriumcsatornákat illeti, a kísérletek alapján egy pozitívan töltött oldallánc, mint például a lizin (K) jelenléte szükséges ahhoz, hogy a csatorna monovalens kationra legyen szelektív. Jelenleg a DEKA (aszparaginsav: -1e, glutaminsav: -1e, lizin: +1e, alanin: semleges) sorrendet tartják legvalószínűbbnek2. Itt a szelektív szűrő töltése összesen –1e, ami a kalciumionok abszorpciója ellen hat, mivel egy kétszeres pozitív töltésű ion felvételével sérül az elektronegativitás. Génmutációs kísérletek azt mutatták, hogy a DEKA sorrendet EEEE sorrenddé változtatva, az ionszelektivitás erőteljesen a kalciumion felé tolódott el, a nátriumcsatorna kalciumcsatornává változott. Ez arra utal, hogy az ionszelektivitást valóban a szelektív szűrő környezete szabályozza.

 

Modell

 

A statisztikus mechanikai számítások, és ezen belül a Monte Carlo szimulációk mindig csak egy valamilyen jól definiált modellre végezhetők el. Minél egyszerűbbek ezek a modellek, annál könnyebben vizsgálhatók, annál kisebb a számítógépes szimulációk időigénye. Bár a mai számítógépek és az egyes membránfehérjékre eddig rendelkezésre álló szerkezeti ismeretek lehetővé teszik nagyon részletes, atomi szintű modellek felállítását és az ezeken alapuló százezres részecskeszámú, hónapokig futó szimulációk végrehajtását is, egyszerű modellek használata sokszor célravezetőbb, több okból is. Egyrészt, lehetővé teszi több szimuláció végrehajtását egy szélesebb koncentrációtartományban, és az ionszelektivitás vizsgálatához éppen ez szükséges. Másrészt egyszerű modellek segítségével a rendszer egy-egy jellemző tulajdonságát ragadhatjuk meg.

Jelen esetben, ahogy azt az előző fejezetben már kifejtettük, egy olyan mechanizmust tesz-telünk, amely kizárólag az ionok töltésén és méretén keresztül határozza meg a szelektivitást. (Természetesen a valóság sosem ilyen egyszerű, de a jelenség teljes megértése felé nagy lépést teszünk, ha megmutatjuk, milyen mértékig felelős azért két olyan alapvető tulajdonság, mint pl. az ionok töltése és mérete.) Ezért az ionokat töltött merev-gömbökkel modellezzük (az ionátmérők a 2. táblázatban találhatók). Az oldószer korpuszkuláris természetének elhanyagolása már nagyobb közelítés, de jelen esetben, mint látni fogjuk, célravezető. Ezért az elektrolitot az ún. primitív modellel reprezentáljuk, ahol az oldószer hatását egy dielektromos háttér formájában vesszük figyelembe. További közelítés, hogy az ioncsatornában és az oldatban ugyanakkora dielektromos állandót használunk, a vízre jellemző e=78.5 értéket. Ez a kontinuum modell elhanyagolja, hogy a szelektív szűrőben nyilvánvalóan mások a polarizációs hatások, mint tömbfázisban: az ionok feltehetően a hidrátburkot részben ledobva lépnek be a csatornába. Éppen ennek az energiaveszteségnek a pótlásához szükségesek a szűrőben lévő töltött vagy poláros oldalláncok. A fenti jelenségek vizsgálatára molekuláris szintű szimulációk folyamatban vannak, és a jövőben a kontinuum modell keretein belül is vizsgálni szeretnénk őket egy membránbeli, a tömbfázisétól különböző, attól alacsonyabb lokális dielektromos állandó alkalmazásával10. A dielektromos határfelületeken ébredő polarizációs töltések meghatározására kifejlesztettünk egy numerikus módszert, ami a felületi töltések számítását a felület diszkretizálása után egy mátrixegyenlet megoldására vezeti vissza11.

A szelektív szűrőt egy Rf sugarú merev falú hengerrel modellezzük, a membránt pedig két, egymástól Hf távolságban lévő merev fallal, ahogy az az 2. ábrán látható8,9. A membrán két oldalán két tömbfázis helyezkedik el. Ezek eredetileg a citoplazmának és a sejten kívüli térrésznek felelnek meg, de hangsúlyozzuk, hogy egyensúlyi szimulációkat végzünk. Nem folyik áram, nincs sem koncentráció-, sem potenciálgradiens. Ezért a két tömbfázis egymással ekvivalens, a szimulációs cella a membrán központi síkjára nézve szimmetrikus. A szimulációs cella nagysága z irányban H, periodikus határfeltételt alkalmazunk, míg sugárirányban a cellát egy R sugarú merev henger zárja le. Mind H-nak és R-nek elég nagynak kell lenni, hogy a szimuláció során a merev falaktól elegendően távol homogén tömbfázist kapjunk (a cella dimenzióit a 2. táblázat tartalmazza).

 

2. táblázat

 

Az ionok átmérője és a szimulációs cella dimenziói.

 

Ionátmérők Å-ben

Na+

1.9

Ca++

1.98

Cl-

3.62

O-1/2

2.8

NH4+

3

A szimulációs cella dimenziói (Å)

Rf

5

R

62.5

Hf

10

H

180-400

 

A szelektív szűrő lényegi részét képező aminosav oldalláncokat mozgékonynak feltételezzük. Például a glutaminsavban a karboxilcsoport egy szénlánc végén lóg, mint egy horgonyon. Ez a szénlánc flexibilis, így a végén levő iont joggal feltételezhetjük mobilisnak. (Arról nem is beszélve, hogy az oldalláncok pontos elhelyezkedését a szelektív szűrő körül nem ismerjük, erre vonatkozólag csak feltételezések vannak.) Ezért a karboxilcsoportban lévő oxigéneket két, egyenként –1/2e töltésű (D és E oldalláncok) merevgömbbel, a lizinben (K) lévő +1e töltésű aminocsoportot egy ammóniumionnal modellezzük (az ionátmérők megtalálhatóak a 2. táblázatban). Az alanin (A) oldalláncát külön nem vesszük figyelembe. Ezek az ionok tehát szabadon mozoghatnak a szelektív szűrőn belül, de abból nem léphetnek ki.

 

 

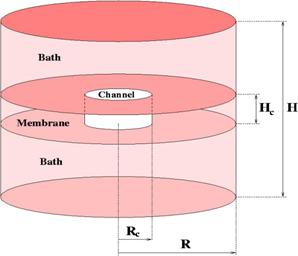
2.       ábra

 

A szimulációs cella.

 

Ahogy már említettük, a szelektivitás valószínűségi fogalom, arra utal, hogy melyik iont milyen valószínűséggel engedi át a csatorna. Ezekben a szimulációkban a szelektivitást egy egyensúlyi abszorpcióval jellemezzük. A kérdés az, hogy melyik ion milyen valószínűséggel tartózkodik a szelektív szűrőben, miközben a tömbfázisban változtatjuk az ionok koncentrációját. A vizsgálat menete a következő: végrehajtunk egy szimulációt tiszta 0.1 M-os NaCl-ra, majd fokozatosan CaCl2-ot adagolunk a rendszerhez miközben a Na+ ionok koncentrációját a tömbfázisban 0.1 M-os állandó értéken tartjuk. Mivel NVT (kanonikus) sokaságú szimulációt használunk, a tömbfázisbeli koncentráció természetesen a szimulációknak végeredménye. Ezért minden esetben egy rövid előzetes szimuláció futtatása szükséges, amelynek alapján a cella hosszát (H) megváltoztatva nagyjából (1%-os hibán belül) állandó nátriumkoncentrációt kapunk.

A Monte Carlo szimulációk részletes magyarázatára itt részletesen nem térünk ki, lényegében egy Boltzmann eloszlás szerint súlyozva mintát veszünk a konfigurációs térből. A szimuláció bemeneti adatai a modellre jellemző mikroszkopikus paraméterek (ionátmérők, töltések), a jelen esetben merev falakkal modellezett külső kényszerek, azaz a cella geometriája, valamint a termodinamikai állapot rögzítéséhez szükséges állapotjelzők (részecskék száma, térfogat és hőmérséklet, T=298K). A szimuláció eredménye a különböző ionok sűrűségprofiljai z függvényében (a rendszer henger-szimmetrikus). Ezekből a sűrűségprofilokból integrálás útján számíthatók a tömbfázisbeli koncentrációk, valamint az, hogy melyik típusú ionból átlagosan hány tartózkodik a szűrőben.

 

Eredmények

 

A kalciumcsatornára kapott szelektivitási görbék a 3. ábrán láthatók8. A szelektív szűrőben 8 oxigénion van. A szelektív szűrőben abszorbeált Na+ és Ca++ ionok átlagos számát ábrázoltuk a tömbfázisbeli kalcium- és nátriumion koncentrációk logaritmusának függvényében. Látható, hogy a csatorna erősen kalciumszelektív. Amikor az oldatban még százszor kevesebb kalciumion van, mint nátriumion, a csatorna már ekkor több kalciumiont abszorbeál, mint nátriumiont. A valóságban a kalciumcsatornák még ennél is szelektívebbek. Ez a modell további finomításának szükségességét jelzi.

 

 

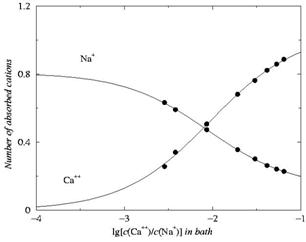
3.       ábra

 

A kalciumcsatorna (EEEE-locus) szelektivitási görbéi.

 

A kalciumcsatornák esetében, modellünk szerint, a kalciumszelektivitást az okozza, hogy a szelektív szűrőben nagy az ionsűrűség, és a jelen lévő negatív töltéseket a kalciumionok, kétszeres töltésük révén, hatékonyabban tudják semlegesíteni. Áttérve a szelektív szűrő körüli DEKA aminosav elrendezésre, reményeink szerint egy nátriumra szelektív csatornához jutunk. Ekkor 4 oxigén, és 1 ammóniumion helyezkedik el a szelektív szűrőben. A szelektivitási görbék a 4. ábrán láthatók9.

 

 

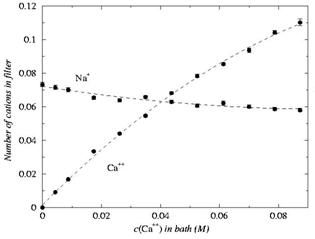
4.       ábra

 

A nátriumcsatorna (DEKA-locus) szelektivitási görbéi.

 

Itt az x-tengelyen a kalciumionok tömbfázisbeli koncentrációját ábrázoltuk. Látható, hogy ha a kalciumkoncentráció elég magas (0,04M), ez a csatorna is kalciumszelektívvé válik, de ez a koncentráció jóval a fiziológiai kalciumkoncentráció (1-2 mM, lásd 1. táblázat) felett van. Azaz, élettanilag releváns körülmények között a csatorna valóban nátriumcsatornaként viselkedik.

 

Szimulációink megmutatták, hogy a kalcium- és nátriumcsatornára rendelkezésre álló strukturális információk alapján egy leegyszerűsített modell állítható fel. Erre a modellre elemi statisztikus mechanikai módszerekkel kapott szelektivitási görbék kvalitatív módon megfelelően reprodukálják azt a viselkedést, amit az illető csatornáktól elvárunk. A modell továbbfejlesztése révén, elsősorban a polarizációs hatások részletesebb leírásával, a jövőben a kísérleti adatokkal még inkább egyező eredményeket kaphatunk. Nem egyensúlyi módszerek (pl. molekuladinamika) segítségével a csatornák vezetési mechanizmusa is tanulmányozható lesz.

 

Köszönetnyilvánítás: a közleményben található eredmények egy nemzetközi együttműködés keretein belül születtek. Ezúton mondok köszönetet Douglas Hendersonnak és David Busathnak (Brigham Young University, Provo, USA), Wolfgang Nonnernak (Univer-sity of Miami School of Medicine, Miami, USA), Bob Eisenbergnek és Dirk Gillespienek (Rush Medical College, Chicago, USA).

 

Ajánlott irodalom:

 

1.       Alberts, Bray, Johnson, Lewis, Raff, Roberts, Walter: Essential Cell Biology, Garland Publishing, Inc. New York & London, 1998.

2.       Hille, B.: Ionic Channels of Excitable Membranes, Sinauer Associates, Inc.: Sunderland, MA, 2001.

3.       Tieleman, D. P., Biggin, P. C., Smith, G. R., Sansom, M. S. P.: Simulation Approaches to Ion Channel Structure-Function Relationships, 2001, Quaterly Reviews of Biophysics, 34, 473.

4.       Doyle, D. A., Cabral, J. M., Pfuetzner, R. A., Kuo, A., Gulbis, J. M., Cohen, S. L:, Chait, B. T., MacKinnon, R.: The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity, 1998, Science, 280, 69.

5.       Nonner, W., Catacuzzeno, L., Eisenberg, B.: Binding and Selectivity in L-Type Calcium Channels: A Mean Spherical Approximation, 2000, Biophysical Journal, 79, 1976.

 

Publikációk a témakörben:

 

6.       Boda, D., Busath, D. D., Henderson, D., Sokolowski, S.: Monte Carlo Simulation of the Mechanism for Channel Selectivity: The Competition Between Volume Exclusion and Charge Neutrality, 2000, J. Phys. Chem. B 104, 8903.

7.       Boda, D., Henderson, D., Busath, D. D.: Monte Carlo Study of the Effect of Ion and Channel Size on the Selectivity of a Model Calcium Channel, 2001, J. Phys. Chem. B 105, 11574.

8.       Boda, D., Henderson, D., Busath, D. D.: Monte Carlo Study of the Selectivity of Calcium Channels: Improved Geometrical Model, 2002, Molecular Physics, 100, 2361.

9.       Boda, D., Busath, D. D., Eisenberg, B., Henderson, D., Nonner, W.: Monte Carlo Simulations of Ion Selectivity in a Biological Na Channel: Charge Space Competition, 2002, Phys. Chem. Chem. Phys., 4, 5154.

10.   Boda, D., Varga, T., Henderson, D., Busath, D. D.,  Nonner, W., Gillespie, D., Eisenberg, B.: Monte Carlo simulation study of a system with a dielectric boundary: Application to calcium channel selectivity, 2004, Mol. Sim., 30, 89.

11.    Boda, D., Gillespie, D., Nonner, W., Henderson, D., Eisenberg, B.: Computing induced charges in inhomogeneous dielectric media: Application in a Monte Carlo simulation of complex ionic systems, 2004, Phys. Rev. E, 69, Art. No. 046702.

 


* Készült az MTA VEAB Fizikai Munkabizottságának ülésére. 2002. április 16. Berzsenyi Dániel Fősikola, Fizika Tanszék, Szombathely; Módosítva az MTA Elméleti Fizikai Kémiai Munkabizottságának ülésére. 2002. október 2. MTA Kémiai Kutatóközpont, Budapest; Jelen kiadvány számára kiegészítve. 2005 január