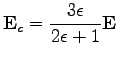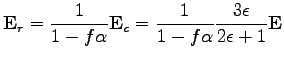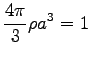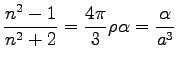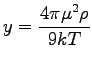

Next: A dielektromos állandó számítása
Up: A dielektromos állandó klasszikus
Previous: A reakciótér
Most már csak az irányító térre kell egy összefüggés.
Ezt egy kis okoskodással könnyen kiszámíthatjuk.
Az irányító tér megkapható, ha gondolatban eltávolítjuk a permanens dipólust, de megahgyjuk a polarizálhatóságot.
Hagyjuk, hogy a környezet adaptálja magát a helyzethez, majd rögzítsük a környezet töltéseloszlását.
Ekkor távolítsuk el a központi molekulát.
A belső tér a üregben épp az irányító tér lesz, mert a permanens dipólus eltávolítása révén épp annak reakcióterét,
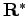 -ot hagytuk ki, tehát a teljes belső térből ezt kivonva az irányító tér marad.
Ezt sokszor elvégezzük és sokaságátlagot vonunk.
-ot hagytuk ki, tehát a teljes belső térből ezt kivonva az irányító tér marad.
Ezt sokszor elvégezzük és sokaságátlagot vonunk.
A probléma megoldása, hogy távolítsuk el a polarizálhatóságot is.
Ekkor egy gömb alakú üregünk van 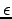 dielektromos álloandójú közegben
dielektromos álloandójú közegben
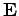 külső térben.
Jól ismert elektrosztatikai probléma.
Megoldása az üregben az ún. üregtér:
külső térben.
Jól ismert elektrosztatikai probléma.
Megoldása az üregben az ún. üregtér:
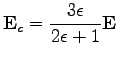 |
(103) |
Ha most bekapcsoljuk a polarizálhatóságot, ehhez hozájön az indukált dipólus (
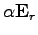 ) által létrehozott reakciótér is (
) által létrehozott reakciótér is (
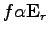 ):
):
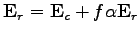 |
(104) |
amiből
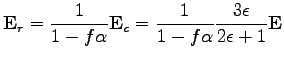 |
(105) |
Ezt behelyettesítve a belső és az irányító tér közötti összefüggést leíró egyenletbe (102), majd az eredményt a mesteregyenletbe (92), kapjuk
![$\displaystyle \dfrac{(\epsilon-1)(2\epsilon+1)}{12\pi\epsilon}= \rho\dfrac{1}{1-f\alpha} \left[ \alpha + \dfrac{\mu^{2}}{3kT} \dfrac{1}{1-f\alpha} \right]$](img230.png) |
(106) |
Hogy egy használhatóbb alakot kapjunk, csinálni kell valamit az 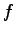 -et tartalmazó tagokkal, amiben szerepel a üreg sugara
-et tartalmazó tagokkal, amiben szerepel a üreg sugara 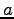 , ami egy meglehetősen ködös mennyiség.
A levezetés során Onsager a következő közelítést javasolta:
, ami egy meglehetősen ködös mennyiség.
A levezetés során Onsager a következő közelítést javasolta:
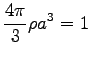 |
(107) |
ami azt jelenti, hogy az üreg térfogata megegyezik a molekula térfogatával.
Ez persze közelítés, főleg folyadékban.
Felhasználjuk továbbá a Lorentz-Lorentz egyenletet, mely szerint
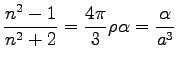 |
(108) |
Ez hasonlít a Clausius-Mosotti egyenlet és tulajdonképpen a nagyfrekvenciás dielektromos állandót adja meg (
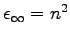 ), mert nagy frekvencián az orientációs polarizáció kikapcsol, a poláros anyag pedig apolárosnak látszik.
Ezt használva egy halom algebrával megmutatható, hogy
), mert nagy frekvencián az orientációs polarizáció kikapcsol, a poláros anyag pedig apolárosnak látszik.
Ezt használva egy halom algebrával megmutatható, hogy
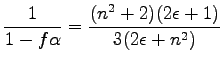 |
(109) |
Ezt a beírva 106 egyenletbe és rendezve kapjuk az Onsager-egyenletet:
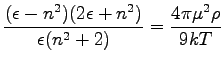 |
(110) |
A jobb oldalon álló mennyiséget dipóluserősség-függvénynek nevezzük és 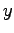 -nal jelöljük:
-nal jelöljük:
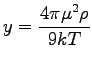 |
(111) |
Ha feltesszük, hogy a molekulák nem polarizálhatók (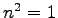 ), akkor azt kapjuk, hogy
), akkor azt kapjuk, hogy
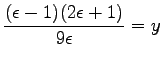 |
(112) |
Erre az egyenletre később még visszatérünk.
Mivel az Onsager-egyenlet a reakcióteret is figyelembe veszi, ezért folyadékokban is érvényes, de csak gyengén polárosakban.
Hiányossága, hogy molekulát körülvevő többi dipólus hatását csak kiátlagolva, egy kontinuum-közelítés keretein belül veszi figyelembe.
Levezetésénél csak a klasszikus elektrosztatikát és egy egyszerű linearizált Boltzmann-statisztikát (meg egy-két közelítést) vettünk igénybe.
A szomszédos molekulák sok-sok lehetséges kölcsönös helyzetben lehetnek egymáshoz képest.
Minden ilyen helyzetben különbözik a molekulák egymésra gyakorolt orientáló és polarizáló hatása.
Ahhoz, hogy ezt számolni tudjuk, fejlettebb statisztikus fizikai elméletre van szükség.
A követkeő részben megtanuljuk, hogyan számolhatjuk a dielektromos állandót egy molekuláris szimuláció keretein belül.


Next: A dielektromos állandó számítása
Up: A dielektromos állandó klasszikus
Previous: A reakciótér
Dezso Boda
2006-08-30
![]() -ot hagytuk ki, tehát a teljes belső térből ezt kivonva az irányító tér marad.
Ezt sokszor elvégezzük és sokaságátlagot vonunk.
-ot hagytuk ki, tehát a teljes belső térből ezt kivonva az irányító tér marad.
Ezt sokszor elvégezzük és sokaságátlagot vonunk.
![]() dielektromos álloandójú közegben
dielektromos álloandójú közegben
![]() külső térben.
Jól ismert elektrosztatikai probléma.
Megoldása az üregben az ún. üregtér:
külső térben.
Jól ismert elektrosztatikai probléma.
Megoldása az üregben az ún. üregtér: