


Next: A Poisson-egyenlet megoldása
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: Bevezető
Az elektrosztatika két alapegyenlete Maxwell I. és II. törvénye:
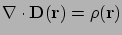 |
(1) |
és
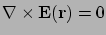 |
(2) |
Az első egyenletben
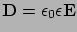 az elektromos eltolás vektora,
az elektromos eltolás vektora, 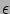 a közeg dielektromos állandója,
a közeg dielektromos állandója,
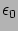 a vákuum permittivitása és
a vákuum permittivitása és
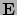 az elektromos térerősség.
Az elektrokémiai kettősréteg alapvető modelljeiben az oldószert egy folytonos dielektrikummal írják le.
Az oldószer a legtöbb esetben víz, aminek a dielektromos állandója
az elektromos térerősség.
Az elektrokémiai kettősréteg alapvető modelljeiben az oldószert egy folytonos dielektrikummal írják le.
Az oldószer a legtöbb esetben víz, aminek a dielektromos állandója
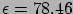 .
Az oldat dielektromos állandója a koncentráció növekedésével csökken, ezt is figyelembe lehet venni.
.
Az oldat dielektromos állandója a koncentráció növekedésével csökken, ezt is figyelembe lehet venni.
A második egyenlet, mely szerint az elektrosztatikus tér rotációja zérus, azt fejezi ki, hogy a tér konzervatív és létezik potenciálja, ami a térerősséggel a következő viszonyban áll:
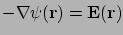 |
(3) |
azaz a térerősség a potenciál negatív gradiense. A negatív előjel megállapodás kérdése, a pozitív ionok abban a térerősség irányába mozognak és a potenciál csökkenésének irányába.
A térerősségből integrálással kapható a potenciál, amiből rögtön következik, hogy a potrenciál csak egy tetszőlegesen választható konstans erejéig meghatározott mennyiség. Ez általában nem okoz gondot, mert amúgy is csak két pont közötti potenciálkülönbségre vagyunk kíváncsiak (a feszültségre).
Ha mégis szükségünk van a potenciál abszolút értékére, választanunk kell egy nullpontot. Triviális választás a végtelen, mint viszonyítási pont, a töltésrendszerünktől végtelen távolságban a potenciál nullához tart. De más választás is lehetséges, a rendszertől függően, az elektrokémiai cellák esetében pl. a standard hidrogénelektód potenciálja a nullpont.
Az elektromos kettősrétegben az elektródot egy végtelen kiterjedésű töltött sík felülettel modellezik, emiatt a rendszer planáris geometriával rendelkezik: a rendszer a felülettel párhuzamos két dimenzióra nézve homogén.
Ezért az 1. egyenlet felírható egy dimenzióban:
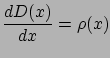 |
(4) |
ahol 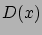 az elektromos eltolás vektorának
az elektromos eltolás vektorának 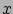 -komponense. Feltéve, hogy a dielektromos állandó konstans, azaz a dielektrikum homogén, ez felírható a potenciál segítségével:
-komponense. Feltéve, hogy a dielektromos állandó konstans, azaz a dielektrikum homogén, ez felírható a potenciál segítségével:
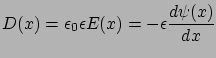 |
(5) |
Ezt az alakot az 4. egyenletbe helyettesítve kapjuk a Poisson-egyenlet 1 dimenziós, a kettősréteg problémára alkalmazható alakját:
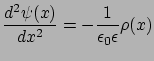 |
(6) |
A Poisson-egyenlet általános alakja
![$\displaystyle \nabla \cdot \left[ \epsilon(\mathbf{r}) \nabla \psi(\mathbf{r}) \right] =-\frac{1}{\epsilon_{0}} \rho(\mathbf{r})$](img21.png) |
(7) |



Next: A Poisson-egyenlet megoldása
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: Bevezető
Boda Dezso
2005-02-17
![]() az elektromos eltolás vektora,
az elektromos eltolás vektora, ![]() a közeg dielektromos állandója,
a közeg dielektromos állandója,
![]() a vákuum permittivitása és
a vákuum permittivitása és
![]() az elektromos térerősség.
Az elektrokémiai kettősréteg alapvető modelljeiben az oldószert egy folytonos dielektrikummal írják le.
Az oldószer a legtöbb esetben víz, aminek a dielektromos állandója
az elektromos térerősség.
Az elektrokémiai kettősréteg alapvető modelljeiben az oldószert egy folytonos dielektrikummal írják le.
Az oldószer a legtöbb esetben víz, aminek a dielektromos állandója
![]() .
Az oldat dielektromos állandója a koncentráció növekedésével csökken, ezt is figyelembe lehet venni.
.
Az oldat dielektromos állandója a koncentráció növekedésével csökken, ezt is figyelembe lehet venni.