


Next: A Gouy-Chapman elmélet
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: A Poisson-egyenlet
A Poisson-egyenlet egy differenciálegyenlet, amit a megfelelő peremfeltételekkel meg kell oldani.
Általában a töltéssűrűségeloszlás ismert, aminek ismeretében meg kell határozni a potenciált.
Ez az egyenlet alkalmasabb a probléma megoldására, mint az I. Maxwell egyenlet (1. egyenlet). mert skaláregyenlet és nem vektoregyenlet.
Tegyük fel, hogy 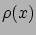 rendelkezésre áll, mondjuk Monte Carlo szimulációval kiszámítottuk.
A kettősréteg esetében a peremfeltételeink a következők:
mind a potenciál, mind a térerősség nullához kell, hogy tartson ahogy
rendelkezésre áll, mondjuk Monte Carlo szimulációval kiszámítottuk.
A kettősréteg esetében a peremfeltételeink a következők:
mind a potenciál, mind a térerősség nullához kell, hogy tartson ahogy
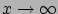 .
.
Megmutatható, hogy a megoldás előáll a következő integrál alakjában:
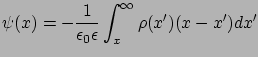 |
(8) |
A bizonyítás egyszerű, kétszer differenciálni kell 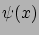 -et, és visszakapjuk a Poisson-egyenletet.
Két tagra bontva a potenciált
-et, és visszakapjuk a Poisson-egyenletet.
Két tagra bontva a potenciált
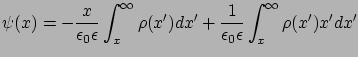 |
(9) |
és differenciálva (az első tagot szorzatként) kapjuk:
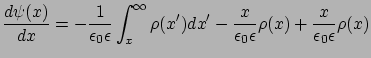 |
(10) |
ahol felhasználtuk, hogy
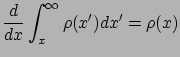 |
(11) |
mivel a deriválás az integrálás inverz művelete.
A 10. egyenletet újra differenciálva előáll a Poisson-egyenlet.
Az elektromos térerősség a 10. egyenletből:
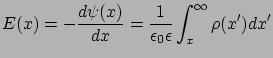 |
(12) |
Ha tehát a töltéssűrűség ismert, numerikus integrálás segítségével a potenciálprofil meghatározható a 8. egyenletből.



Next: A Gouy-Chapman elmélet
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: A Poisson-egyenlet
Boda Dezso
2005-02-17
![]() rendelkezésre áll, mondjuk Monte Carlo szimulációval kiszámítottuk.
A kettősréteg esetében a peremfeltételeink a következők:
mind a potenciál, mind a térerősség nullához kell, hogy tartson ahogy
rendelkezésre áll, mondjuk Monte Carlo szimulációval kiszámítottuk.
A kettősréteg esetében a peremfeltételeink a következők:
mind a potenciál, mind a térerősség nullához kell, hogy tartson ahogy
![]() .
.