A Gouy-Chapman elmélet

A XX. század elején Gouy és Chapman egymástól függetlenül közölték a Poisson-egyenlet megoldását a Boltzmann-eloszlás feltételezésével. Ezért ez tulajdonképpen nem más, mint a Poisson-Boltzmann (PB) egyenlet. A Poisson-egyenlet "vezérli" az elektrosztatikát, a Boltzmann-eloszlás pedig a statisztikus mechanikát. Ugyanez a megközelítés használatos ionok szolvatációjánál tömbfázisban, ahol Debye-Hückel (DH) elméletnek hívják, illetve kolloidkémiában, ahol Derjaguin-Landau-Verwey-Overbeek (DLVO) egyenletnek nevezik. A biofizikában egyszerűen csak Poisson-Boltzmann egyenletnek nevezik. Az elmélet eleganciája és analitikus megoldása miatt még ma is széles körben használják a kísérleti eredmények analizálására.

Az elmélet feltételezi, hogy az ionok ponttöltések. Ez a feltételezés önmagában alacsony koncentrációkra korlátozza az elmélet érvényességi tartományát.

Írjuk fel a Poisson-egyenletet a különböző ionok sűrűségeloszlásainak (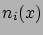$n_{i}(x)$) függvényében:

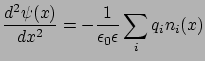$$\frac{d^{2}\psi(x)}{dx^{2}}=-\frac{1}{\epsilon_{0}\epsilon} \sum_{i}q_{i}n_{i}(x)$$ (13)

Feltesszük, hogy ezekre a sűrűség eloszlásokra a Boltzmann eloszlás érvényes:

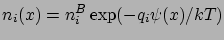$$n_{i}(x)=n^{B}_{i}\exp(-q_{i}\psi(x)/kT)$$ (14)

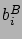ahol $b^{B}_{i}$ az illető komponens sűrűsége a tömbfázisban. Ez az egyenlet annak a valószínűségét adja meg, hogy az illető ion az 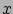$x$ helyen tartózkodik. Ez a valószínűség annak az energiának az exponensével arányos, amit az illető ion az adott helyen felvesz 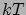$kT$ egységben mérve. Látható, hogy az egyenlet egy összefüggést állapít meg a potenciál és a sűrűség között. A másik egyenlet, ami egy ilyen összefüggést megállapít, az éppen a Poisson-egyenlet. A kettő együtt megoldható.

A fenti Boltzmann-eloszlás megkapható az elektrokémiai potenciálokra vonatkozó egyensúlyi feltételből. Az 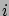$i$-edik szpecies elektrokémiai potenciálja:

$$\mu_{i}=kT\ln \left[ \Lambda_{i}n_{i}(x)\right] + q_{i}\psi(x)$$ (15)

A jobb oldalon az első tag az ideális gáz kémiai potenciálját adja (ne feledjük, hogy a részecskék pontszerűek), a második tag az elektrosztatikus energiát. A kettőből áll össze az elektrokémiai potenciál. A rendszer az elektród közelében egyensúlyban van a rendszerrel távol az elektródtól, azaz a tömbfázissal. A tömbfázisban a kémiai potenciál

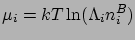$$\mu_{i}=kT\ln(\Lambda_{i}n^{B}_{i})$$ (16)

A tömbfázisban 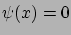$\psi(x)=0$. A két (elektro)kémiai potenciál egyenlőségéből éppen a Boltzmann-eloszlás következik. Vegyük észre, hogy az ionok pontszerűnek való feltételezése kulcsfontosságú. Ha az ionok mérettel rendelkeznének, entropikus tagok jelennének meg. Ezeket a szimuláció magától értetődően szolgáltatja, és ha elmélettel akarnánk kiszámítani őket, egy az elektrosztatikus energiára vonatkozó egyszerű Boltzmann-eloszlásnál fejlettebb statisztikus mechanikai elméletre van szükségünk. Léteznek ilyen elméletek, pl. különböző integrálegyenletek, a főkömbi közelítés, vagy sűrűségfunkcionál-elméletek.

A Boltzmann-eloszlást (14. egyenlet) a Poisson-egyenletbe (13) helyettesítve kapjuk a Poisson-Boltzmann egyenletet:

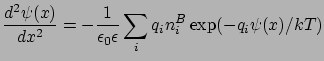$$\frac{d^{2}\psi(x)}{dx^{2}} =-\frac{1}{\epsilon_{0}\epsilon} \sum_{i}q_{i}n^{B}_{i}\exp(-q_{i}\psi(x)/kT)$$ (17)