A Poisson-Boltzmann egyenlet megoldása

Az egyenlet megoldásánál a következő feltételezésekkel élünk:

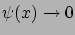$\psi(x)\rightarrow 0$ ha $x\rightarrow \infty$

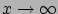
Rögzítsük az elektródpotenciált: 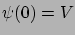$\psi(0)=V$.

Linearizáljuk az egyenletet! Ehhez fel kell tenni, hogy 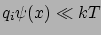$q_{i}\psi(x)\ll kT$. Ekkor az exponenciális Boltzmann-faktor sorbafejthető:

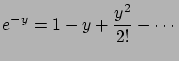$$e^{-y}=1-y+\frac{y^{2}}{2!}-\cdots$$ (18)

Írjuk fel a szummát:

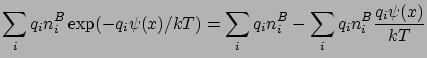$$\sum_{i}q_{i}n_{i}^{B}\exp(-q_{i}\psi(x)/kT) = \sum_{i}q_{i}n_{i}^{B} - \sum_{i}q_{i}n_{i}^{B}\frac{q_{i}\psi(x)}{kT}$$ (19)

A jobboldal első tagja zérus, mivel a tömbfázis elektromosan semleges. Bevezetve a Debye-féle árnyékolási hosszat:

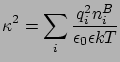$$\kappa^{2}=\sum_{i} \frac{q_{i}^{2}n_{i}^{B}}{\epsilon_{0}\epsilon kT}$$ (20)

a PB-egyenlet a

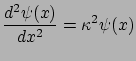$$\frac{d^{2}\psi(x)}{dx^{2}}=\kappa^{2}\psi(x)$$ (21)

alakúra egyszerűsödik. Ennek a megoldása

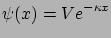$$\psi(x)=V e^{-\kappa x}$$ (22)

Kétszer deriválva könnyen ellenőrizhető, hogy a 22. egyenlet valóban megoldása a PB-egyenletnek. Az is látható, hogy a határfeltételek teljesülnek. Az eredményből a Debye-féle árnyékolási hossz is értelmezhető: az az inverz távolság (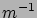$m^{-1}$ dimenziójú), amely alatt a potenciál az 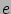$e$-ad részére csökken.

A potenciál visszahelyettesítésével a sűrűségprofilra azt kapjuk eredményül, hogy

$$n_{i}(x)=n_{i}^{B}\left[ 1-\frac{q_{i}\psi(x)}{kT} \right] =n_{i}^{B}\left[ 1-\frac{q_{i}V}{kT} e^{-\kappa x} \right]$$ (23)