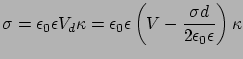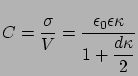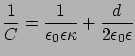Next: Eredmények
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: Szimuláció és elmélet összehasonlítása
A GC elméletnek a fent leírt formájában van egy fontos, de könnyen kiküszöbölhető hiányossága.
Mivel az ionokat pontszerűnek tekintjük, azt is megengedjük, hogy az ionokat reprezentáló ponttöltések az elektródot tetszőlegesen kicsi távolságra megközelítsék. A valóságban ez nyilván nincs így, a töltések az elektródot legfeljebb 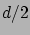 távolságban (az ionok sugara) tudják megközelíteni. Ez a szimulációban nyilvánvalóan teljesül, mert ott az ionokat
távolságban (az ionok sugara) tudják megközelíteni. Ez a szimulációban nyilvánvalóan teljesül, mert ott az ionokat 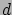 átmérőjű töltött merevgömbökként modellezzük és nem engedjük meg a gömböknek az elektróddal való átlapolódását.
átmérőjű töltött merevgömbökként modellezzük és nem engedjük meg a gömböknek az elektróddal való átlapolódását.
Stern javasolta, hogy a GC elméletben az ionokat továbbra is pontszerű részecskékként modellezük, de ne engedjük meg enkik, hogy az elektródot 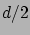 távolságnál jobban megközelítsék. Az elektódhoz közel így kialakult réteget, amelyben töltések nincsenek, de potenciálesés van, Stern-rétegnek nevezik. Használatos a Helmholtz-réteg vagy konpakt-réteg elnevezés is.
távolságnál jobban megközelítsék. Az elektódhoz közel így kialakult réteget, amelyben töltések nincsenek, de potenciálesés van, Stern-rétegnek nevezik. Használatos a Helmholtz-réteg vagy konpakt-réteg elnevezés is.
Egyenleteink ezzel a feltételezéssel nem sokat módosulnak, tulajdonképpen csak eltoljuk a potenciál- és sűrűségprofilokat 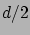 értékkel.
A potenciált hasonlóképpen származtathatjuk, mint fent, csak a referenciapont most nem az
értékkel.
A potenciált hasonlóképpen származtathatjuk, mint fent, csak a referenciapont most nem az 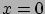 , hanem az
, hanem az 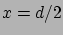 pont lesz. Ebben a pontban legyen a pontenciál
pont lesz. Ebben a pontban legyen a pontenciál 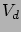 , amit diffúzréteg-potenciálnak nevezünk.
Ekkor hasonló megfontolások alapján kapjuk a potenciálra, hogy:
, amit diffúzréteg-potenciálnak nevezünk.
Ekkor hasonló megfontolások alapján kapjuk a potenciálra, hogy:
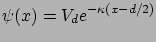 |
(29) |
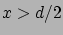 -re.
A diffúzréteg potenciál egyszerűen megkapható a következőképpen.
A Stern-réteg vastagsága
-re.
A diffúzréteg potenciál egyszerűen megkapható a következőképpen.
A Stern-réteg vastagsága 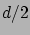 , a térerősség a Stern-rétegben
, a térerősség a Stern-rétegben
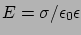 .
A potenciálesés
.
A potenciálesés
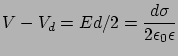 |
(30) |
ahonnan
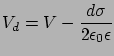 |
(31) |
A potenciálprofil 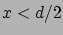 -re lineáris:
-re lineáris:
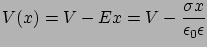 |
(32) |
A sűrűségprofilok pedig:
![$\displaystyle n_{i}(x)=n_{i}^{B}\left[ 1-\frac{q_{i}V_{d}}{kT} e^{-\kappa (x-d/2)} \right]$](img69.png) |
(33) |
Integrálva (most 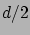 -től
-től 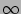 -ig) és a töltéssemlegességi feltételt kihasználva kapjuk:
-ig) és a töltéssemlegességi feltételt kihasználva kapjuk:
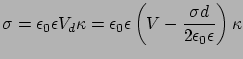 |
(34) |
Rendezve adódik, hogy
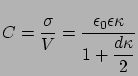 |
(35) |
Vegyük a kapacitás reciprokát és rendezzük:
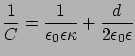 |
(36) |
Ebből az látszik, hogy a teljes rendszer kapacitása előáll, mint két sorbakötött kondenzátor kapacitása. Az első tagot nevezzük a diffúzréteg kapacitásának és látható, hogy megegyezik a GC elmélet által a Stern-réteg nélkül adottal. A másik tag a Stern-réteg kapacitása. Szokásos eljárás az elektrokémiában, hogy ennek a Stern-rétegnek a dielektromos állandóját lecsökkentik, miáltal a kísérletekkel összhangban álló kapacitásértékeket tudnak számolni. A spúrás klasszikus esete, a kísérleti eredmények kiértékelésében mindenesetre még ma is ezt az eljárást használják az elektrokémikusok.



Next: Eredmények
Up: Az elektrokémiai kettősréteg vizsgálata
Previous: Szimuláció és elmélet összehasonlítása
Boda Dezso
2005-02-17
![]() távolságban (az ionok sugara) tudják megközelíteni. Ez a szimulációban nyilvánvalóan teljesül, mert ott az ionokat
távolságban (az ionok sugara) tudják megközelíteni. Ez a szimulációban nyilvánvalóan teljesül, mert ott az ionokat ![]() átmérőjű töltött merevgömbökként modellezzük és nem engedjük meg a gömböknek az elektróddal való átlapolódását.
átmérőjű töltött merevgömbökként modellezzük és nem engedjük meg a gömböknek az elektróddal való átlapolódását.
![]() távolságnál jobban megközelítsék. Az elektódhoz közel így kialakult réteget, amelyben töltések nincsenek, de potenciálesés van, Stern-rétegnek nevezik. Használatos a Helmholtz-réteg vagy konpakt-réteg elnevezés is.
távolságnál jobban megközelítsék. Az elektódhoz közel így kialakult réteget, amelyben töltések nincsenek, de potenciálesés van, Stern-rétegnek nevezik. Használatos a Helmholtz-réteg vagy konpakt-réteg elnevezés is.
![]() értékkel.
A potenciált hasonlóképpen származtathatjuk, mint fent, csak a referenciapont most nem az
értékkel.
A potenciált hasonlóképpen származtathatjuk, mint fent, csak a referenciapont most nem az ![]() , hanem az
, hanem az ![]() pont lesz. Ebben a pontban legyen a pontenciál
pont lesz. Ebben a pontban legyen a pontenciál ![]() , amit diffúzréteg-potenciálnak nevezünk.
Ekkor hasonló megfontolások alapján kapjuk a potenciálra, hogy:
, amit diffúzréteg-potenciálnak nevezünk.
Ekkor hasonló megfontolások alapján kapjuk a potenciálra, hogy:
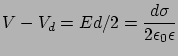
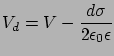
![$\displaystyle n_{i}(x)=n_{i}^{B}\left[ 1-\frac{q_{i}V_{d}}{kT} e^{-\kappa (x-d/2)} \right]$](img69.png)