Eredmények

Vegyünk egy 1:1 elektrolitot ($q_{1}=e$ és $q_{2}=-e$), az ionok átmérője $d=3$ Å $=3\times 10^{-10}$ m, a koncentráció $c=1$M=1 mol/dm$^{3}$, a hőmérséklet $T=295.15$ K, a dielektromos állandó $\epsilon =78.46$.

A szimuláció bemeneti paramétere az elektródtöltés, ez legyen $\sigma=-0.1$ C/m$^{2}$.

Eredményeinket gyakran redukált egységekben adjuk meg. PL. a töltést nem Coulombban, hanem $e$-ben, ez elemi töltésben mérjük, a hosszúságot méter helyett ionátmérőben ($d$). A potenciált ekkor megadhatjuk $kT/e$ egységben. Egy elemi töltés energiája a potenciáltérben $e\psi$, ez energia dimenziójú mennyiség. Dimenzió nélküli mennyiséget kapunk, ha ezt $kT$-hez viszonyítjuk.

A felületi töltéssűrűséget (töltés/felület) C/m$^{2}$-ben mérjük, a redukált töltéssűrűséget pedig így kapjuk: $\sigma^{*}=\sigma d^{2}/e$. A fenti -0.1 C/m$^{2}$ redukált egységben $\sigma^{*}=-0.05617$

A sűrűség SI mértékegysége db/m$^{3}$, a redukált sűrűség $n^{-}=nd^{3}$. Látszik, hogy ez a $d^{3}$ térfogatú kockában lévő részecskék száma. Ez akkor lenne egy, ha a részecskék köbös rácsban egymást érintve helyezkednének el. Ennél valójában a redukált sűrűség lehe nagyobb, mert a pakolás lehet ennék szorosabb, még folyadék fázisban is. Ebben az esetben azonban, mivel az oldószermolekulákat nem kezeljük explicite, a sűrűség csak az ionok parciális sűrűsége. Ez egy kis mennyiség (gáz jellegű): $n_{i}^{B}*=0.0163$.

Ezután nézzük az eredményeket. A szimuláció az adott $\sigma$-hoz megadja a potenciált, az adott rendszerre ez egzakt eredménynek tekinthető. Ez az érték $eV/kT=-2.212$, ami -0.0568 V-nak felel meg. A GC (annak Stern-féle kiterjesztése) elmélet esetében választhatunk, hogy a szimuláció által adott elektródpotenciált, vagy az elektródtöltést használjuk független változóként. A két esetben különböző eredményeket kapunk. A sűrűségprofilok a következő ábrán láthatók:

Látszik, hogy a GC eredmények a két esetben némileg különbözőek. Rögzített elektródtöltésnél ugyanazt az eredményt kapnánk, ha a MC és a GC töltésprofilokat integrálnánk, tudniilik az elektródtöltést (lásd 24. egyenlet). Szembetűnő, hogy a GC anionprofilok negatívvá válnak. Ez nyilvánvalóan fizikailag értelmetlen eredmény, a linearizálás eredménye. A PB egyenlet a töltéssűrűséggel dolgozik, az erre kapott görbék nem rosszak, a kation- és anionprofilokra külön-külön a linearizált Boltzmann-eloszlás nem dolgozik túl jól.

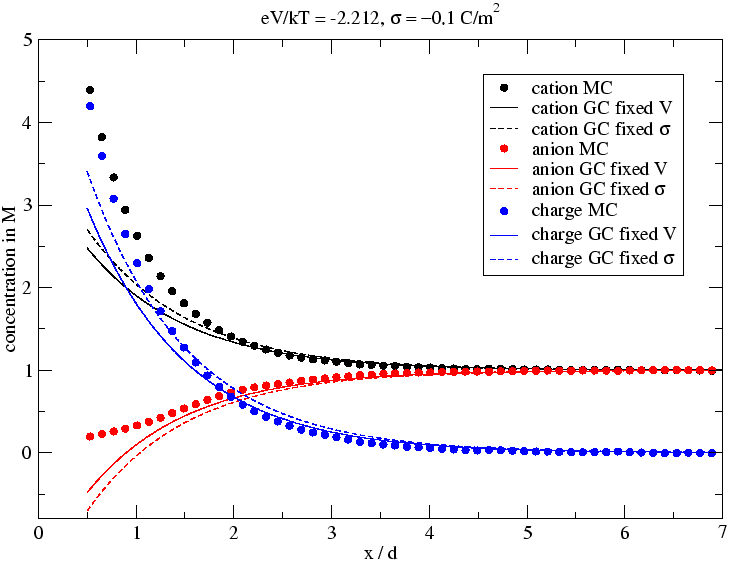
A potenciálprofilok (amik a sűrűségprofilból kétszeres integrálással állnak elő) viszont nem rosszak, ahogy a következő ábra mutatja:

Az rögtön látszik, hogy rögzített elektródpotenciálnál az MC és GC potenciálok értékei $x=0$-ben megegyeznek, ahogy ezt előírtuk. Rögzített elektródtöltésnél az egyezés kevésbé jó.

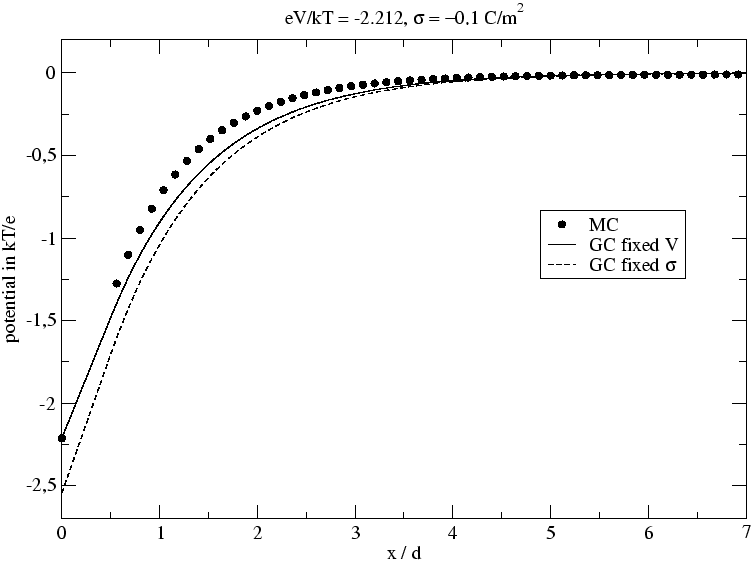
Ha ugyanezeket a számításokat végigcsinánánk kisebb koncentrációra (mondjuk, 0.1 M-ra), jobb egyezést tapasztalnánk a GC elmélet és a szimulációk között. Mindezekről bővebben lehet olvasni a következő cikkben: Boda D, Fawcett WR, Henderson D, Sokolowski S: Monte Carlo, density functional theory, and Poisson-Boltzmann theory study of the structure of an electrolyte near an electrode, JOURNAL OF CHEMICAL PHYSICS, 116 (16): 7170-7176, 2002.